Sat Dec 18, 2021 False Tissot Images
Updated on Mon Jan 10, 2022
A short confession
I have to tell you something that I should have told you long ago: The Tissot indicatrix images that I’m showing for each and every map projection that I’m presenting here… actually are false Tissot indicatrices – sort of a pseudo Tissot indicatrix! 😳
The images are not using real Tissot ellipses but small circles – more specifically, distance circles (circles of equal distance from a given point) –, to visualize the projections’ distortions. The good news is: That doesn’t effect the sense and purpose of the images; you still can use them to inspect and analyze the kind and distribution of distortions in any given map projection! It’s just that they depict this slightly different, and that I’ve been using the wrong appellation for them.
Furthermore, the difference between small circles and the Tissot ellipses is enormously important when you want to calculate distortion values of a projection, as e.g. done by the Airy-Kavraiskiy criterion that I’ve metioned repeatedly during the last months. However, my images aren’t supposed to be used for calculations of any kind, but merely for a visualization of distortions. In this regards, they serve well.
And basically, that’s all I wanted to tell you today.
However, I’m the chatty guy, so in case you’re interested, read on to learn
the exact difference between small circles and the Tissot indicatrix and
why I’m not using the latter on my website.
A long explanation
Part 1: The difference
So what’s the difference between small circles and Tissot ellipses? In the Tissot article I wrote a few year back, I said:
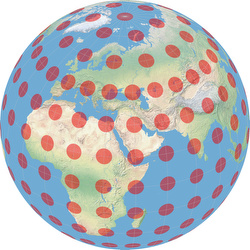
Imagine someone painting a lot of circles of identical size, at regular intervals, onto the Earth’s surface. When he’s done with it, the Earth viewed from space will look like shown in the image below.
Actually, that is a description of small circles, not Tissot ellipses!
Each of the circles shown in the image above has a radius of roughly four degrees for longitude, which
equals 444 kilometers or 276 miles. So someone painted really huge circles onto the earth.
The real Tissot ellipses, however, are infinitesimal, i.e. too small to be measured, approaching zero.
Now of course, an infinitesimal ellipse can’t be seen, which kind of puts a dent in the purpose
to visualize distortion, doesn’t it? So the Tissot ellipses are magnified after they have been computed.
You could say that the ellipses and the map are shown at different scales.
In a nutshell, the difference is that Tissot ellipses show the distortion at certain
infinitesimal points on the map, while the small circles show the distortion
of an area on the map, namely the full area that is covered by the respective circle.
Now, let’s get on to the visual repercussions of that difference. For many projection, the divergence is marginal. Look at this example of the Winkel Tripel projection, with the red filled dots being the small circles that I’m using on all the images, and the blue outlined ellipses being the real Tissot indicatrix:
At this size, you’ll probably think that they are absolutely identical. But look at this detail from the northwestern “corner” of the map:

In the upper row, at 75°N, you now can see the differences. If you look closely, you can also spot differences in the lower row: At the northeastern part of each ellipse, the blue outline is within the area of the red dot, while at the southwestern part, it’s on the outside.
So this deviations are hardly worth mentioning – at least, not for the images on my website. But here’s another example of the pseudo and the real Tissot indicatrix in the Hobo-Dyer projection:
I guess the difference ist fairly obvious – nonetheless, here’s a detail of the “ellipses” in the pseudo Tissots near the South pole:

You can see that the red dots actually are no ellipses: The northern boundary has a different curvature than the southern,
which makes dots in the upper row kind of “egg-shaped” and the lower row, ummm… I don’t know what to call that shape.
The reason for that is that the angular distortions of the Hobo-Dyer projection rapidly increase as you approach the poles
(since it’s an equal-area projection, there are no areal distortions anywhere on the map).
At the northern vertex of the (deformed) small circle in the bottom of the above image,
the angular deformation is 30°, while at the southern vertex, it already has reached roughly 77°.
With such a difference within the circle, it’s hardly surprising that it gets bent to a shape
that’s no longer an ellipse.
In contrast, this kind of deformation can not be observed using the real Tissot indicatrix.
Again, no surprise here – since the real Tissot ellipses are infinitesimal, there is no difference of the angular distortions
within any given ellipse:

So now you know the difference between the pseudo and the real Tissot indicatrix. One questions remains…
Part 2: Why do I keep using the pseudo Tissot indicatrix?
When I started to work on my website about six years ago, I didn’t even know
that the images I’m providing are pseudo Tissot indicatrices. But now that I’m aware of this
(and like I said in the beginning, for some time already), why keep I using them instead
of replacing them with the real Tissot images?
The thing is, I’m using five different applications to render all the projection images on my website:
Geocart,
G.Projector,
Flex Projector,
MapDesignerRaster,
and
d3-geo-projection scripts.
All five can project a plate carrée world map to other projections. The input map I use for the “Tissot” images, looks like this (the graticule line are later added by the map projection software):
You can see again that this map shows the “non-ellipses” near the poles because they are actually small circles. So I always used a wrong input image. But it would also make no difference if these were the real Tissot ellipses: Projecting an image will never result in the true Tissot indicatrices, because they have to be computed specifically for each projection.
And why don’t I do that then?
Because of the five programmes mentioned, only two are capable of doing this:
Geocart and Flex Projector. For images created by Geocart, I would be a bit
of work to make them look the the images I’m using so gar (i.e. red dots, yellow continents etc).
Using Flex projector exports, I would be a lot of work.
And then, I still wouldn’t have real Tissot indicatrices for the projections
rendered by one of the other three applications.
Much work, little gain.
Because with the small circles the distortion patterns can also be well
evaluated visually when using the small circles. And that’s why
I’ll keep using them.
One more thing …
Almost four years ago, I started using new “Tissot” images; but only for newly added projections. At that time, I wrote: “the existing Tissot images will not be replaced”. Well, guess what – recently I started to replace them after all. I have already done about 90, and I still have just as many to go.
I’m going to do this bit by bit (without further notice), so it will be a while before I’m done with it.
Update Jan 10, 2022:
Two notes. First off – Peter Denner to the rescue again!
He showed me how
“to draw a micron-sized Tissot ellipse, which is as close to an infinitesimally small one as makes no odds” using the
d3 scripts. So basically, I now could render real Tissot ellipses for all projection images made by d3, too.
But sorry, I still won’t do that, for the reasons given above.
Secondly, the old pseudo Tissot renderings
have now been replaced by the new ones for all projections!
So they are still false Tissots, but at least now in a uniform graphic representation.
Comments
2 comments





 Except where otherwise noted, images on this site are licensed under
Except where otherwise noted, images on this site are licensed under
Tobias Jung