Sat Aug 20, 2022 Second Serving: Two More Lee Variants
Updated on Fri Sep 09, 2022
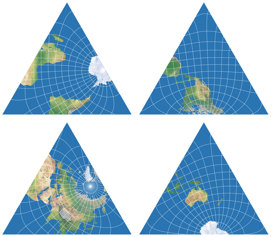
Three weeks ago, I presented the original and two rearrangements of the conformal tetrahedral projection by L.P. Lee. And a few days ago I remembered that there are two more variants. Both of them rearrange the four faces of Lee’s tetrahedron to show the world in half a regular hexagon, but use different projection centers.
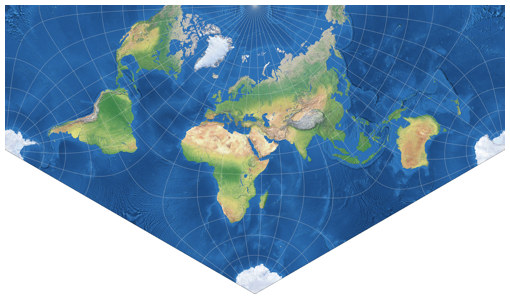
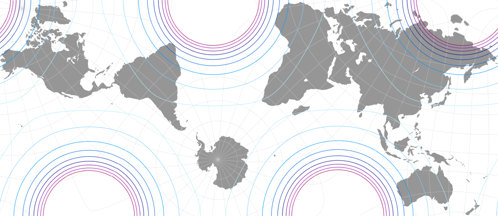
I found the first one
on
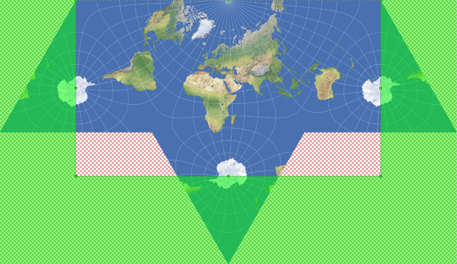
Carlos Furuti’s website. It was introduced in 2004 by Constant Xarax from Greece[1] and is using the original south polar aspect, centered at 20°W.
The positioning of the continents still is quite familiar compared to standard maps,
although it separates Alaska from the rest of the North American continent and spilts up
Antarctica into three parts.
Furuti labelled the projection “Xarax’s world in half of a regular hexagon”, but I added it
to my Projection Collection using the name Lee-Xarax.
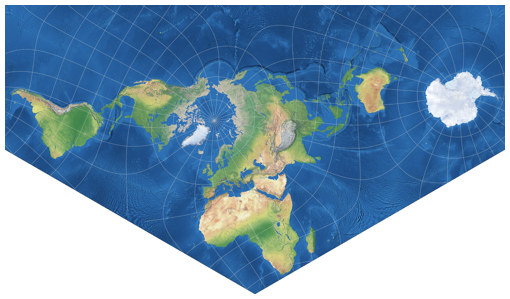
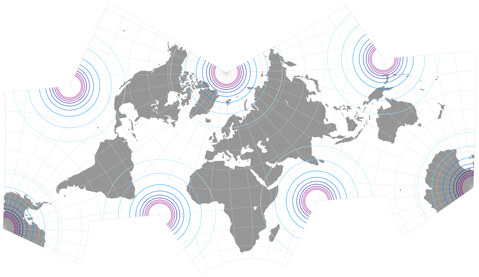
The second one was presented to the public
in the Mapthematics forum,
posted in 2020 by its creator Luca Concialdi.
The positioning of the continents surely is unusual, but it shows all of them uninterrupted and
keeps the distortions away from land areas very well. When arranging his variant, Concialdi didn’t think of
Xarax’s prior work but he doesn’t exclude the possibility that he might have remembered it unconsciously.[2]
He proposed the name “Lee conformal tetrahedral projection – Concialdi rearrangement”,
but since that is a bit too long to listed on my website, he agreed to the use of the appellation
Lee-Concialdi.
So, here they are:
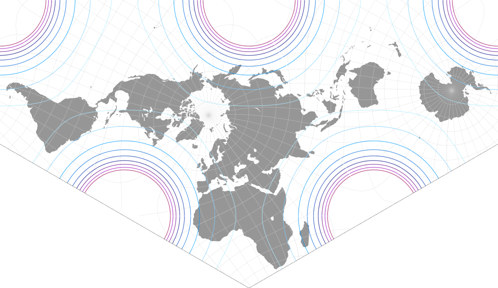
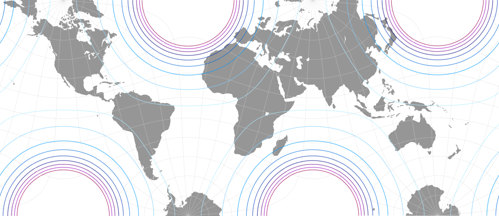
Let’s have a look a the usual visualization of distortions, i.e. the areal inflations.
Apart from the two new projections I’ll also repeat the two Lee variants presented recently,
namely Markley and CALM, but I’ll also throw in Concialdi’s earlier work Cahill-Concialdi
that I
presented in 2019 (although that is
not based on an tetrahedral, but an octahedral projection).
The lines represent values of
1.2; 1.5; 2.0; 2.5; 3.0; 3.5; 4.0; 4.5; and 5.0:
This time I will dispense with the “this is better here and that is better there” type comments and leave the analysis to you. Suffice it to say that both projection have a very favourable distribution of areal inflation, regrettably their outer shape probably limits the possibilities of practical use. Nonetheless I think both are fine conformal world maps.
I kept the review quite short intentionally – because now, I’d like to describe the construction of both maps, and that will take some time…
Construction of Lee-Xarax & Lee-Concialdi
Currently, there seems to be no software that can render either of the two projections out of the box.
[Update Sep 9, 2022: There is a software, see below.]
But there are at least two applications that offer Lee’s conformal tetrahedral projection,
so you can assemble the variants by Xarax and Concialdi yourself:
Geocart (commercial) and
MapDesignerRaster (free).
The first steps differ in these two.
MapDesignerRaster renders a full-world representation of Lee’s projection.
Select the projection Lee tetrahedral (triangular).
For Lee-Xarax the configuration parameters are:
Latitude: 90
Longitude: -20
Ctr. Meridian: 0
For Lee-Concialdi the values are:
Latitude: 37
Longitude: 168
Ctr. Meridian: -81
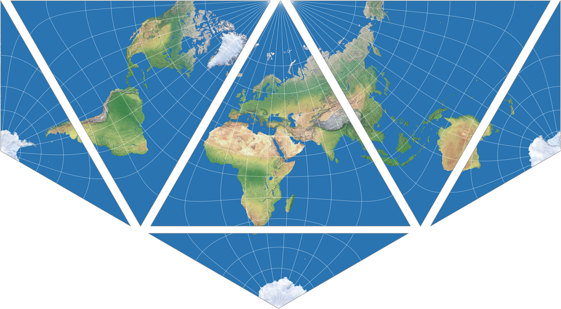
Save the file as PNG image and open it with a graphics application. You now have to cut the equilateral triangle into four smaller equilateral triangles. The center face then has to be split up into three isosceles triangles of equal size.
Cut edges in the Lee-Xarax (left) and Lee-Concialdi projections:
Cut along the solid lines first.
Then subdivide the center face along the dotted lines.
I’ll show the assembly of the parts later. First, I’d like to explain the first steps in Geocart. As I’ve already said in the blogpost mentioned in the beginning, this application renders the four faces of the tetrahedron separately.
Create a new map using the polyhedral conformal face projection.
Call up the Projection Parameters dialogue, select the Platonic solid tetrahedron.
Set the Face to 0.
Then, call up the Projection Center dialogue. For Lee-Xarax, enter the following values:
Latitidinal: 90°S
Longitudinal: 20°W
Transversal: 0°
For Lee-Concialdi:
Latitidinal: 37°S
Longitudinal: 12°W
Transversal: 99°
Copy the map and paste it three times.
For the three copies, enter the Faces 1, 2, and 3 in the Projection Parameters dialogue.
Your document should now roughly look like this:
The center triangle (holding the south pole on Lee-Xarax and parts of Antarctica, South Amerika and Afrika on Lee-Concialdi) now has to be cut into three equal parts as shown above.
Regardless of which programm you used, you should now have all six pieces of the puzzle. Put them together according to this template (shown only for the Lee-Xarax, I guess you can figure out which parts are to be put where in the Lee-Concialdi):
To me, the hardest part was to split the center face into thirds. So here are two alternative approaches. The first only works in Geocart and is (as far as I can tell) applicable to Lee-Xarax only.
You may have noticed that the cut edges exactly run along certain
meridians. This allows us to have the programm do the tripartite division.
You’re going to need three instances of the center face.
Call up the Boundaries dialogue for all three consecutively.
Make sure the button “Boundaries are defined relative to the graticule” is checked.
For all three, enter the boundaries North: 15°S and South: 90°S.[3]
For the eastern and western boundaries, you have to set different values on each instance, namely
West: 20°W and East: 100°E,
West: 100°E and East: 140°W, and
West: 140°W and East: 20°W.
And voilà, there are the three parts you need!
The other alternative works with both projections and the result of both applications. Instead of cutting up the center face, you have to duplicate it twice and then put the faces together like this:
After you’ve put them together seamlessly, remove the parts that are not needed on the left, right and bottom. On the Lee-Xarax that’s fairly easy because all cuts must pass right through the south pole:
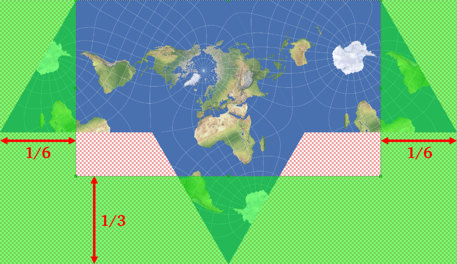
On the Lee-Concialdi you don’t have such a convenient visual help, so you have to do a bit of math. If your image has any borders around the actual projection, remove them first. Then, cut off a sixth of the image’s width on the left and the right edges and a third of the image’s height at the bottom:
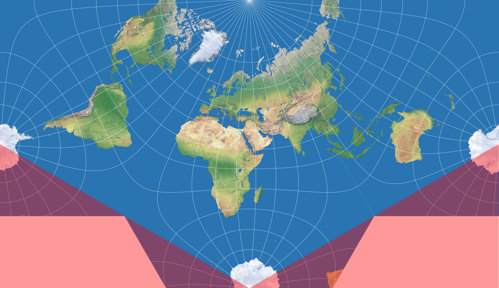
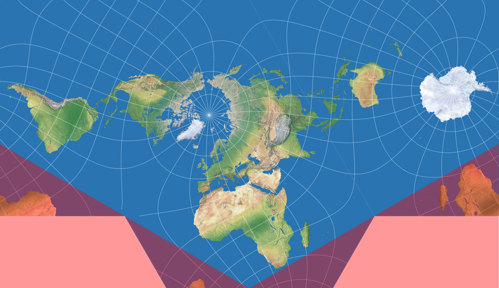
In the final step, you have to remove two parts of triangular shape. This can be a problem because many application do not offer a triangular selection tool. So here’s what I did: I opened the file in a vector graphics editor (Adobe Illustrator, Affinity Designer, PhotoLine, Inkscape etc.) and drew two triangles on top of the image. The vertices have to be set in the left and right lower corners, at the vertical center on the left and right edges, and at the horizontal center at the bottom edge. Again, these points are exactly at the south pole on the Lee-Xarax. Here’s an example for both projections, using red semi-transparent triangles. In fact, they should naturally be opaque and filled with the desired background colour:
Phew! We’re finished!
One more hint: Putting the pieces together really seamlessly is well-nigh impossible
– or I’m being particularly clumsy about it. Could be.
But I recommend to build a map that is considerably larger than you actually need it and then scale it down
to the desired size. With a bit of luck, that will hide the seams. For a perfect
result, you might “repair” a bunch of pixels…
P.S.: I had just finished writing this blogpost when I saw that Lee’s tetrahedral conformal projection is available for d3, namely in d3-geo-polygon. Using the Observable demo, I found out that the aspect for Lee-Xarax can be created using .rotate([-40, 0]). I have not yet been able to find the correct input values for Lee-Concialdi and will probably not investigate further. If somebody else finds them, feel free to tell me. However, the construction process for the finished maps will be the same as shown for images rendered by MapDesignerRaster.
🌐
Update Sep 9, 2022:
Constant Xarax pointed me to the
Flexify Photoshop plug-in
which can render a wide range of projections (albeit a lot of them are for decorative use only),
among them the Lee-Xarax (simply called Xarax there).
I don’t have Photoshop, but downloading the free trial version of the plug-in, I could
see that it also runs with the applications PhotoLine and Affinity Photo.
And since Flexify offers settings for Latitude, Longitude and Spin, you should
be able to render Lee-Concialdi, too. I’m saying “should” because I didn’t
find the exact values for that variant.
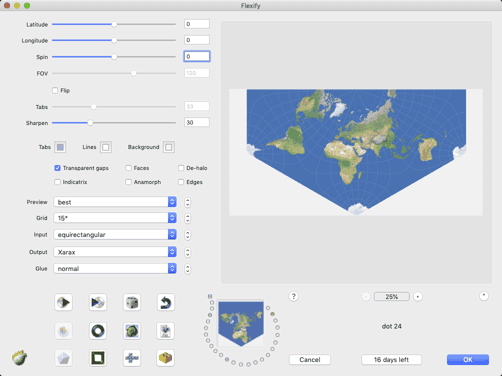
The Lee-Xarax projection gets rendered when you select “Xarax” as output and leave the settings for Latitude, Longitude and Spin at 0, which of course differs from the values I’ve noted above, but I think this is comprehensible, because here, it just means “use the default center of this projection”.
So in order to render Lee-Concialdi, it seemed logical to me
to input the deviation of its projection center from Lee-Xarax’.
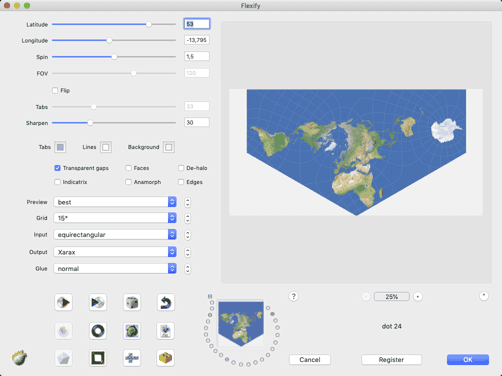
However, this didn’t work. The closest approximation I could find
(and it still isn’t the real thing) was created with the values
Latitude: 53
Longitude: -13.795
Spin: 1.5
I don’t have a logical explanation for this, but – as far as I can tell – you really need values with decimals to arrive at Lee-Concialdi. And therein lies a problem, because each time I wanted to type in two fractional values, some kind of input validation seemed to kick in an e.g. changed -13.8 to -138 or 1.5 to 1. I have no idea if this is a general bug of the plugin or if it’s because I’m not calling it from Photoshop. In any case, the only way for me to enter two fractional values was not to type them in, but to set them using the sliders. But then, it is quite impossible to set accurate values. That’s why you can see the -13.795 in the screenshot above: Actually, I wanted to try -13.8, but I was glad that I ended up nearby.
So I just stopped trying to render Lee-Concialdi accurately. But I think it is possible. Somehow. Anyway, the advantage of the Flexify plug-in is that don’t have to do all the work shown above – cutting, pasting, hiding the seams. But remember that is is a graphical tool, no cartographic or GIS software. So if you want to create a real map with labels for countries, cities or physical features, you can use Flexify to create the backdrop image, but the rest has to be done manually.
But of course, in a blogpost about the Lee-Xarax and Lee-Concialdi projections, the Flexify plug-in is worth mentioning.
References / Footnotes
- ↑ Regrettably, Furuti didn’t mention the source of Xarax’s proposal. If anyone knows more about it, please tell me!
- ↑ Cited after personal communication in August 2022.
- ↑ Actually, North: 15°S is only an example. It works with any parallel that is outside of the given triangle across its entire length.
Comments
One comment
Constant Xarax
I would like to add just a few comments on this "World map on half a regular hexagon" - as Carlos Furuti himself used to call the world map projection I had proposed back in 2004.
a. My main idea was that, in order to get a conformal projection with as few noticeable land-mass distortions as possible, the North hemisphere should better be represented in some two-fold way ( well, if we still wish to keep, and map, Russia in one piece anyway :) :) ), but the South hemisphere was crying for a three-way ( due to the those three large land masses there, Africa, South America and Australia ). So, keep the North Pole in one place, and divide the South in three.
b. I decided that, to achieve that, splitting Alaska from the rest of the North American continent was a relatively small price to pay ( given that nowadays it belongs to a separate country from Russia or Canada, and the international border lies mostly along this looong, nice, cartographically convenient meridian... :) ). This is the main compromise of this map. I would suggest that one should better arrange the map so that this particular meridian, 141 W, is its left end one.
c. "Half a regular hexagon" is an easy to conceptualize and remember polygon, and it fits well into modern wide-aspect monitors.
Now, if we don t mind to separate Siberia in two parts, instead, we can use a conformal projection with three regular hexagons in a row.
A joke that I was not been able to see it coming... Some guys "discovered" ( I have no idea how on earth they managed to do this...), that the central meridian of this map was pretty close to the meridian of their Holy city - and you may guess what they thought after that :). I let this pass.
Thank you, and, please, continue your good work.
Constant Xarax
Athens, Greece.






 Except where otherwise noted, images on this site are licensed under
Except where otherwise noted, images on this site are licensed under
Tobias Jung
It’s always great to get a few words from the original creator, which (for obvious reasons) isn’t possible for most of the projections listed on my website.
Thanks again, and kind regards,
Tobias
Alexandre Canana
Alexandre Canana
Tobias Jung
Well, check out the September part of my calendar series! ;-)
https://blog.map-projections.n…
Alexandre Canana