Two more Wagner Variants

Tue Jan 15, 2019 Two more Wagner Variants

Yes, I know: This site ist called map-projections.net, not wagner-projections.net, and I’ve already got 26 Wagner variants in the list, so why add another two?
Well˛ I’ve got my reasons, and I’ve got reasons to do it now but for the lack of time, I’ll just introduce them briefly and will come back to the matter in greater detail at some point in the future (but that’ll take some time).

Thr Basic Idea

As I mentioned on several occasions^[1], Karlheinz Wagner designed his »Hammer projection with a pole line« (later labelled Hammer-Wagner or Wagner VII) to be customizable in terms of
a) the length of the pole line,
b) the curvature of the parallels,
c) the aspect ratio of the main axes, and
d) the amount of areal inflation (including no inflation at all, i.e. equal area).

Regarding a, b and c, the Wagner VIII is identical to Wagner VII, the only difference is that while the VII is equivalent, Wagner defined an areal inflation by 1.2 at 60° N/S.

Now, I really like certain projections by Frank Canters (namely Canters W13 and W14), G. A. Ginzburg (Ginzburg V and VI), and Oswald Winkel (Winkel Tripel, original version and Bartholomew’s variant) but I also feel that they’ve got a considerable amount of areal inflation near the poles.
(More accurately: The difference between the amount of areal distortions at the center of the map and in polar areas is a bit too large for my liking.)
Being incapable of developing my own projection formulae, I came up with the idea to customize the Wagner VIII to obtain a projection that would bear a certain resemblance to the aforementioned projections but with a lesser amount of areal inflation. Its working title was Wagner CGW-A (CGW for Canters, Ginzburg, Winkel, A for aphylactic, a rarely used term for compromise projections). Moreover, I wanted to provide him with an equal-area twin brother, just like Wagner himself did it the other way round.

I came to results I liked, but then I realized that
1) the aphylactic version didn’t look very much like Ginzburg’s projections, but was quite close to Dr. Rolf Böhm’s Wagner variation called Wagner-Böhm I; so I decided to drop the G from the name and add a B instead;
2) simply removing the areal inflation would not result in an equal-area projection I liked, so I also adjusted the curvature of parallels and the ratio of main axes. Thus, they’re not actually twin brothers anymore, but I guess (and hope) you still can see a »family resemblance«.

Without further ado: Here are the Wagner BCW-A I and the Wagner BCW-E (E for equivalent or equal-area, whatever you prefer).

Note (March 26, 2021): The BCW-A I was originally introduced as Wagner BCW-A. I added the roman numeral i>I later, see here.

Wagner BCW-A I

Areal inflation equals 1.27 at 60° N/S, the Böhm notation is 67-80-60-27-190.
Let’s have a look at the distortion characteristics:

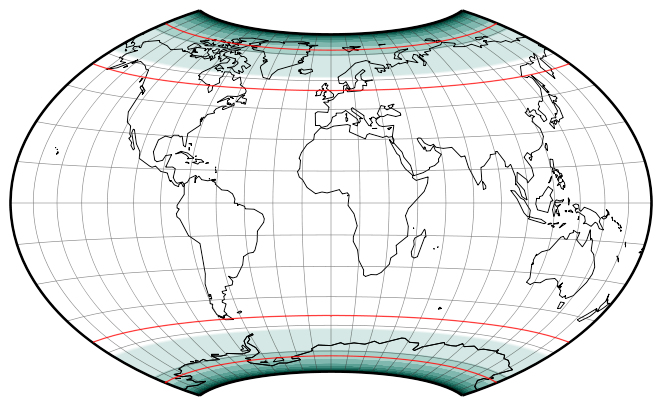
Areal distortion patterns of the Wagner BCW-A I.
Lighter hues mean less distortion. Darker hues mean more distortion.
The red lines mark an areal inflation by 1.2 and 2.0.

Angular distortion patterns of the Wagner BCW-A I.
Lighter hues mean less distortion. Darker hues mean more distortion.
The red lines mark the maximum angular distortion of 40° and 80°.

Wagner BCW-E

Böhm notation: 67-85-60-0-198.
Being an equal-area projection, we’ll just need the visualization of the angular distortions:

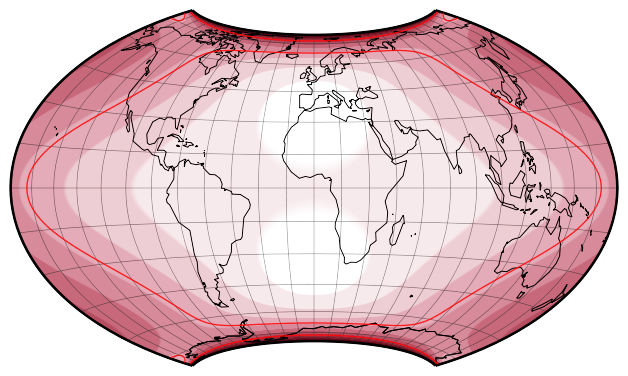
Angular distortion patterns of the Wagner BCW-E.
Lighter hues mean less distortion. Darker hues mean more distortion.
The red lines mark the maximum angular distortion of 40° and 80°.

By the way – here’s another variant. In order to get it closer to Winkel Tripel, I compressed it a bit horizontally (while preserving equivalence). But in my opinion, I’m leaving the area of a decent display of Africa here, because it’s too stretched in north-south direction.
Therefore I’m not adding it to the list on my website. Nonetheless I’d like to show this variant, which I’ll call Wagner BCW-E₂ for now. Maybe you even prefer it?

Closing Words

I like both BCW-A I and BCW-E – well, of course I do since they were tailored to my liking – and I think both are suitable for general reference world maps, depending on whether you prefer compromise or equal-area projections for this kind of maps.