Wed Jan 15, 2020 Wagner II, lenticular variant
Updated on Mon Feb 03, 2020
Arrggh.
Time and again, I’m saying that I already got too many Wagner variants in the
list of projections – and time and again, I’m adding new ones.
At least this time, I’ve decided that sometime soon I’ll check if I should remove some of them again…
Of course I had the idea for the projections I’m going to show today when I was working on the January sheet of my projection calendar, which shows the Wagner II, a pseudocylindric projections with sinusoidal meridians. As I’ve said, I like this kind of meridian shape – and there’s something else that I like, namely lenticular projections which have curved parallels as opposed to the straight parallels of the pseudocylindricals. But as far as I know, there are no lenticular projections with sinusoidal meridians. So I wanted to see how a thing like that might look.
Using Flex Projector, I was able to create one by
mixing the Wagner II with the bending of the parallels of the Wagner VII.
A description of the mixing process is provided below.
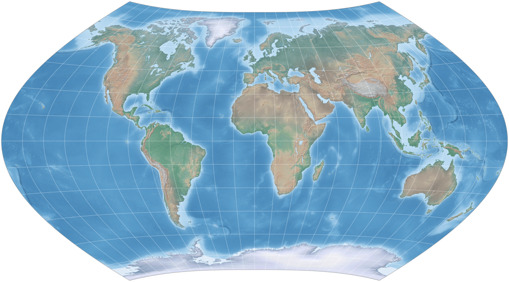
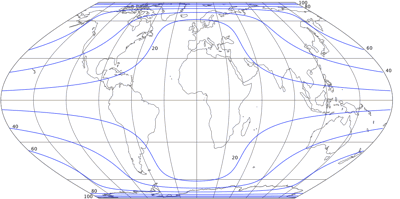
Lenticular Wagner II
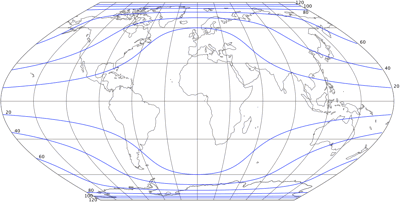
And here it is, the lenticular variant of Wagners II – sinusoidal meridians and curved parallels! It’s certainly nothing special or surprising, but that’s not was I was going for, I just wanted to see how it looks. And I think it is a nice alternative to the original. Now, projections usually don’t use curved meridians to please my eye, but to improve the distribution of distortions. Let’s have a look at a distortion visualization (as exported by Flex Projector) of the original Wagner II and compare it to the lenticular variant, starting with areal distortions:
My variant departs from equivalence even more than the original. As you can see,
the original’s areal inflation at the center of the map is 1 (= equal area),
while the lenticular version has a slight areal deflation (0.88).
Now, the decision on which parts of the map are deemed as inflated or deflated
is somewhat arbitrary [1],
but that doesn’t change the fact that my version has a higher variance in areal distortion values.
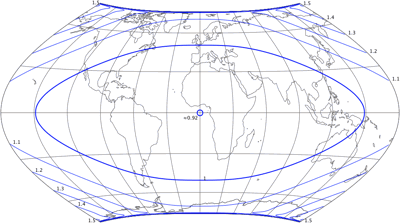
Huh? Didn’t I say something about improvement? Yes I did, but I referred to
angular distortions:
The »corners« of the map (Alaska, eastern Siberia, Japan, New Zealand) benefit from the curved parallels. Since the Wagner II is a compromise profitieren that keeps quite close to equivalence it seemed reasonable to me to allow a slight additional departure from being equivalence to allow the decreased angular distortions. At least judging by the values given in Flex Projector (there are other metrics which might give other results!) in total, it is an improvement:
| Projection | Scale | Scale Cont. | Areal | Areal Cont. | Angular | Angular Cont. | Acc. |
|---|---|---|---|---|---|---|---|
| Wagner II lenticular | 0.27 | 0.30 | 0.17 | 0.22 | 23.74 | 24.52 | 82.7 |
| Wagner II original | 0.32 | 0.35 | 0.12 | 0.16 | 26.88 | 27.88 | 76.5 |
Emphasized values are better. For an explanation of the values, see below. [2]
So now I had a sinusoidal lenticular projection and it has
at least some advantages over the original. You can compare them directly:
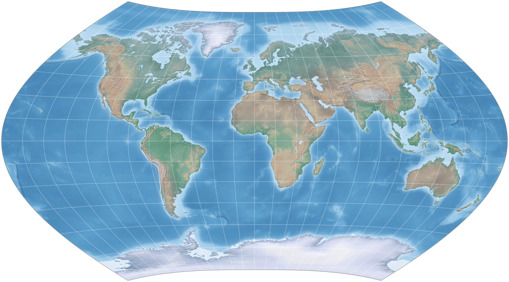
Wagner II original vs. Wagner II lenticular
The link triggers the “Expert Mode” and jumps to the “scaled to same width” comparison which is
more appropriate here.
But my curiosity wasn’t satisfied so far. Now, I wanted to try lenticular version of Wagner I and Wagner III, to…
Lenticular Wagner I.a
First things first: Here, I mixed the Wagner Im again with the bending of the parallels of the Wagner VII.
And although both projection are equal-area, the result is not!
It’s an aphylactic (= compromise) projection. Since equivalence is an important property, I thought it’s inappropriate to
use the same name – thus, I called it Lenticular Wagner I.a (with a for aphylactic).
We dont’t need a areal distortion visualization for the original (because it has none) but for the lenticular variant I’m showing the inflation at 0.1 intervals to emphasize that it isn’t equivalent:
For the angular distortions, we can compare both version again:
We see the same kind of improvement as above.
In numerical values:
| Projection | Scale | Scale Cont. | Areal | Areal Cont. | Angular | Angular Cont. | Acc. |
|---|---|---|---|---|---|---|---|
| Wagner I.a lenticular | 0.34 | 0.37 | 0.07 | 0.08 | 28.57 | 29.39 | 76.6 |
| Wagner II original | 0.39 | 0.44 | 0.00 | 0.00 | 31.92 | 33.06 | 71.2 |
Emphasized values are better. For an explanation of the values, see below. [2]
The Acc. value doesn’t rise as much as on the Wagner II which is no surprise
since we’ve introduced areal inflation into the projection. Still, it is a bit of an improvement
but you have to decide if that is worth dropping the equivalence.
Frankly, I don’t think so. When I want equivalence, I want real equivalence. If I can feel that I can depart
from it, I can go for the Wagner II to furtherly improve on the angular distortions. Of course it’s
possible to create a lenticular Wagner I that’s truly equal-area. But I have to admit that
I’m not the one who can do it.
Lenticular Wagner III.a
Without ado: Again, the projection loses its property, namely the equally spaced parallels along the central meridian – that’s why I again added the a. Which might be a bit confusing since on my website I listed all projections with equally spaced parallels as »compromise projections«. Oh well… at least (I hope) the suffix clearly shows that there has to be another difference than the curved parallels.
If you like the Wagner III because of its amount of areal inflation, the lenticular variant might be a good alternative. If you like it because of the equally spaced parallels, forget the lenticular Wagner III.a!
For its distortions:
| Projection | Scale | Scale Cont. | Areal | Areal Cont. | Angular | Angular Cont. | Acc. |
|---|---|---|---|---|---|---|---|
| Wagner III.a lenticular | 0.26 | 0.30 | 0.32 | 0.44 | 20.41 | 21.80 | 85.1 |
| Wagner III original | 0.28 | 0.32 | 0.30 | 0.43 | 22.68 | 23.82 | 77.9 |
Emphasized values are better. For an explanation of the values, see below. [2]
Résumé
Well, now I know how lenticular projections with sinusoidal meridians look. That’s a win.
Besides that… well, the variants of Wagner I and III lose (in the implementation shown here)
their metric properties of equivalence and the equally spaced parallels, respectively. Thus they
are no recommendable alternatives to the originals. Since the Wagner II has no metric
properties of that kind, it can’t lose them. 😉
I like this one because it improves on the angular distortions, while the worsening of the areal
distortion doesn’t matter much here (we already are in field of compromise projections).
For this reason, only the lenticular Wagner II will be added to the list of projections
Regarding that a survey performed a few years ago [3] revealed that map readers strongly prefer elliptical over sinusoidal meridians, I strongly doubt that anyone besides myself would be interested in actually using a projection like that. Especially since another result of the survey was that curved meridians aren’t well-liked either (although I never quite understood that conclusion, but that’s a different subject).
But what of it?
This was an experiment in the first place and not all experiments are successful. And there have been projections
before which were created for academic reasons.
(We’ll see an example of that in the June part of my little calendar series).
How I generated them
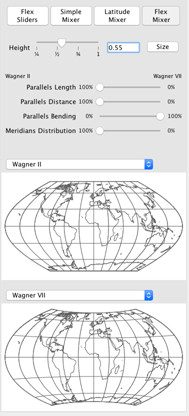
As announced at the beginning, I’d like to show how I mixed the projections. Use the following steps in Flex Projector:
- Switch to the Flex Mixer.
- Select Wagner II as first and Wagner VII as second projection.
- Drag the slider Parallels Bending to 100% Wagner VII.
- Drag the other three sliders to 100% Wagner II.
-
I didn’t like the initial height/width ratio, so I added a little modification here:
Set the Height to 0.55. -
Finally, I hit the Size button and selected Minimize Area Distortion.
Note that this doesn’t actually change the projection, it just sets the (internal) scale factor. This should always be the last step when you create projections in Flex Projector.
Except for the selection of projections in step 2 I applied the same procedure for the lenticular Wagner I and III.
Footnotes
-
↑
On areal inflation/deflation being arbitrary, see the manual of the application Geocart.
You can download the manual for free.
Chapter Distortion Visualization, page 9.18 (= page 140 of the PDF). Read the two paragraphs
starting with:
To understand what these diagrams mean, note that angular deformation is absolute (…) -
↑
↑
↑
Values presented in the distortion table – quoted from Flex Projector’s Help files:
Scale – The weighted mean error for overall scale distortion.
Scale Cont. – The weighted mean error for overall scale distortion. Continental areas only.
Areal – The weighted mean error for areal distortion. 0 indicates equal-area projections.
Areal Cont.– The weighted mean error for areal distortion. Continental areas only.
Angular – The mean angular deformation index. 0 indicates conformal projections.
Angular Cont. – The mean angular deformation index. Continental areas only.
Acc. – The Acceptance index. The relative area with acceptable distortion properties, taking both angular and areal distortions into account.
All continental values are computed for the standard central meridian at Greenwich.
The computation of distortion parameters is based on Frank Canters and Hugo Decleir (1989), The World in Perspective - A Directory of World Map Projections, Wiley, Chichester, etc., 181 p.
The acceptance index is based on Capek, R. (2001), Which is the best projection for the world map? Proceedings of the 20th International Cartographic Conference ICC, Beijing.
Available online -
↑
Bojan Šavrič, Bernhard Jenny, Denis White & Daniel R. Strebe (2015), User preferences for world map projections, Cartography and Geographic Information Science.
Available online
Comments
One comment
Peter Denner
If you mix Wagner III with Wagner IX instead of Wagner VII, do the parallels stay equally spaced?









 Except where otherwise noted, images on this site are licensed under
Except where otherwise noted, images on this site are licensed under
Tobias Jung
can’t tell because Flex Projector doesn’t offer Wagner IX. :-(