Four Flexify Projections and Gott-Wagner

Fri Nov 25, 2022 Four Flexify Projections and Gott-Wagner

A few weeks ago, I mentioned the Flexify Photoshop plug-in, which can render a whole lot of map projections. There a some that well-known projections that I have also listed in my Projection Collection (e.g. Hammer Projection, Winkel Tripel, Robinson Projection, Strebe 1995 etc.), and there are numerous projections which are suitable for decorative purposes only – or, rather, for other purposes than a flat map (e.g. Cube, Rind 1, Shark 3, or Sphericon 8/2). But I also found some that I found interesting enough to add them to my collection.
Let’s check them – and also, another projection that has nothing to do with Flexify.

Three Conformal Hexagonal Projections

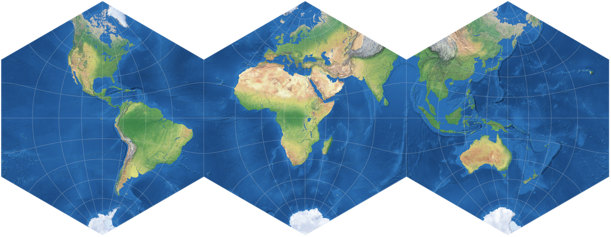
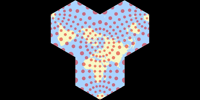
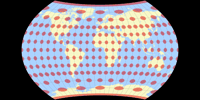
At first, I found… umm, no. I didn’t “find” anything, Contant Xarax pointed me to the Anthracene projection, a conformal map built of three regular hexagons in a row, named after the figure of the chemical structure of a polycyclic aromatic hydrocarbon. You can get a quite advantageous configurations with this one, e.g. when centered to 30°E, the worst areal inflations are kept away from land… mostly, anyway: Brazil, Northeast India, Myanmar give me a bit of a headache, but overall, it’s alright.

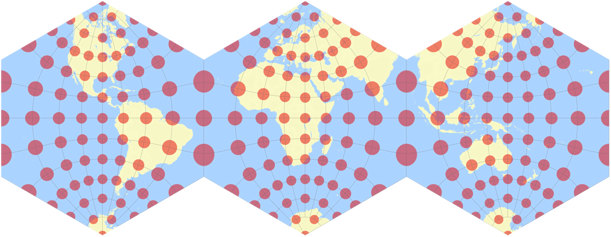
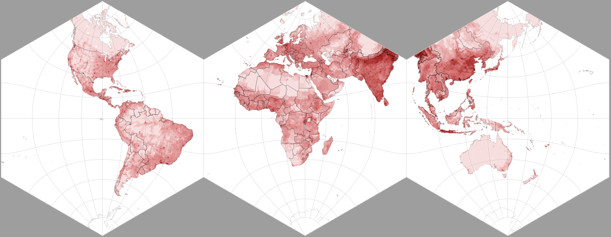
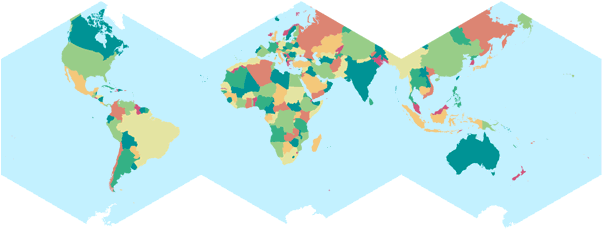
I’m not very pleased about that nasty cut through Asia, especially since (as you can see on the population density map) it runs through some heavily populated areas.

Because of that cut, I first decided that I will not add the Anthracene projection to my collection, but as you can see, I changed my mind: It is an interesting configuration and this website is not about my personal preferences.
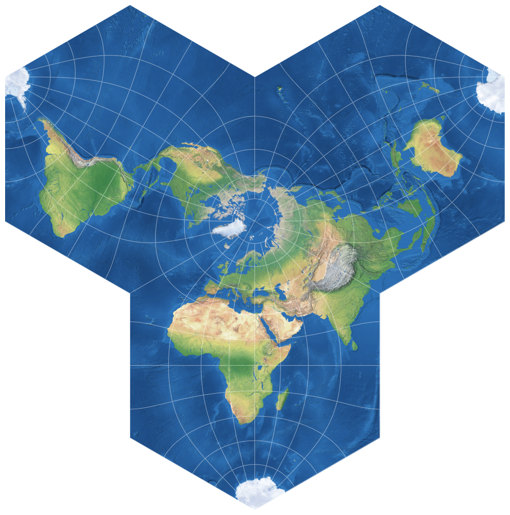
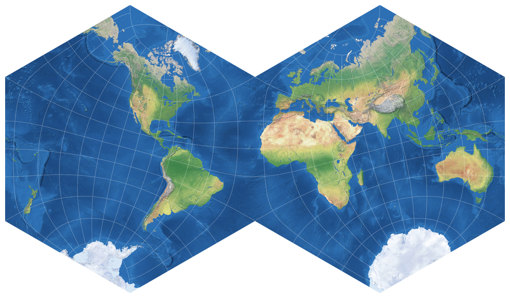
Then I saw that Flexify also has the Phenalene projection (again name after the chemical structure), which uses the same three hexagons as the Anthracene, but arranges them differently and thus, avoids the cut. Usually I prefer the equatorial over the polar aspect, but in this case I will make an exception. So, the Phenalene projection, centered to 90°N/30°E, was added to my Projektion Collection:

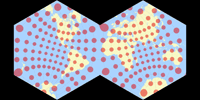
There is another conformal hexagonal projection in Flexify’s library that I like, the Naphtalene projection (and if you think you already can guess how that one got its name – yes, you’re right). Here, the world is displayed in two hexagons. My preferred projection center is 15°N/20°W:

I think the distribution of areal inflations over the continental areas is very fine! Yes, New Zealand gets inflated visibly, and Australia’s got a slight “hunch”, but both drawbacks are less obtrusive than in the Guyou projection that I added a few years ago. (Admittedly, that’s more a consequence of the latitudinal center at 15°N rather than of the projection it self.) If you can put up with the unusual shape, it’s in my opinion a highly usable conformal world map projection.

And then, I found another projection of a different kind in Flexify. And I’m tempted to say: I was destined to find it interesting… 😉

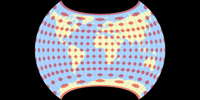
An Aphylactic Lenticular Projection

When I saw the Curvy projection in Flexify’s listing, I instantly thought: “This looks like an umbezifferte Wagner!” At first glance, I thought it might be a Wagner IX variant, but then I realized that it doesn’t have equally spaced parallels along the central meridian: The distances slightly decrease towards the poles. So, if at all, it had to be a Wagner VII variant, like ~~some~~ most of my own experiments.

I started to play with the customizable Wagner’s configuration parameters, and with vii@51.5-102.5-60-64-180 (noted using the Böhm notation)^[1], I arrived at a very good approximation. It doesn’t match to a 100%, but it’s close enough to be sure that the distortion patterns of Flexify’s original will hardly differ. Here is my approximated result:

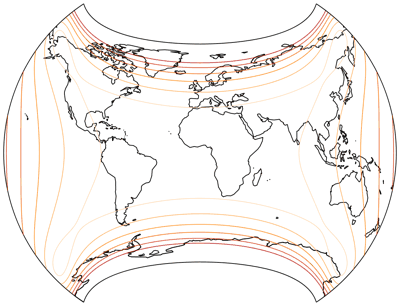
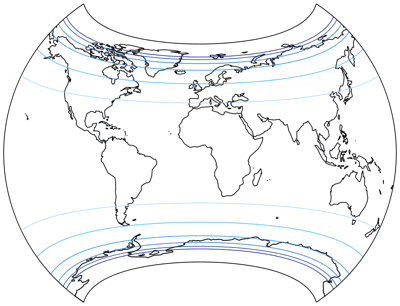
Using the approximation instead if the image rendered by Flexify has various advantages for me: I can continue to create images of this projection once the Flexify trial period has expired, I can make them look exactly like all the other images on my website (note that the graticule of the conformal projections above looks a bit different), and I can create visualizations of the distribution of distortions:

The isolines are given for max. angular deformation of:
10°, 20°, 30°, 40°, 50°, and 60°.
For the areal inflation, shown normalized to the value at the central point of the map, the lines represent values of:
1.2; 1.5; 2.0; 2.5; 3.0; and 3.5.

That’s really not bad, especially Alaska and Eastern Sibiria come off better than in… well, probably any other projection (in equatorial aspect, centered at or near the Greenwich meridian) that I know of. However, the labrys-like shape may limit the possible uses. By the way, the projection is captioned “labrys” in the Flexify gallery, but I preferred to list it using the less martial name.
In Geocart, my approximation can be rendered using the generalized Wagner with the parameters
a = 1.749934, b = 1.745197, m = 0.988142, m2 = 0.58192, n = 0.569444 ;
in the d3-geo-projections scripts, it’s
d3.geoWagner().poleline(51.5).parallels(102.5).inflation(64).ratio(180)

So much for the Flexify projections.
Meanwhile, my free trial period of the plug-in in has expired. It is a great and highly recommendable tool if you want to create illustrations of various map projections (such as all the images I’m showing in my Projection Collection) and is, in my opinion, reasonably priced. On the other hand, it lacks any functions you’d need to create real maps (e.g. with labels, positioned at the right geographic coordinates) and – regarding the fact that I already use five different map projection tools – offers too few projections of the kind that I find interesting and can’t be rendered with any of the other tools. So I decided not to purchase Flexify. However, if you’re interested in creating map projection images, you should give it a try. It is offered as Photoshop plug-in but I could successfully use it in PhotoLine and Affinity Photo (version 1.x, I couldn’t try it anymore using the new Version 2). It’s not unlikely that it’ll run if any other application that supports Photoshop plug-ins.

On to the final projection for today!
When I assumed that the Curvy projection is a Wagner IX variant, I realized that I had forgotten something…

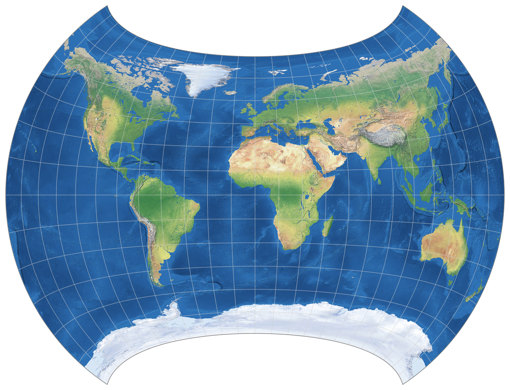
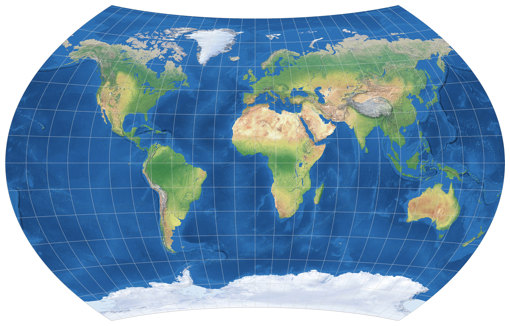
Gott-Wagner Projection

I wanted to add this projection to my collection months ago, but somehow it slipped my mind… 😳

The Gott-Wagner projection was developed by J. Richard Gott III, first shown in 2010^[2] and formally introduced in 2021^[3]. It is a modification of Wagner IX^[4], aimed at beating the Winkel Tripel in terms of overall distortion values measured by the Goldberg-Gott metric^[5]. The Böhm notation reads ix@60-52-450-38.5, using rounded values for the second and the fourth parameter^[6].

Regardless of the question whether it really is an “improvement” on the Winkel Tripel (the advantage of the values is marginal, and other metrics may come to different results), it’s definitively a fine projection, suitable for a lot of a lot of uses.

Among the lenticular aphylactic projections already listed, the Frančula XIII probably has the greatest similarity. The length of the pole line and the ratio of the main axes are quite similar in the two, but Frančula’s projection has a considerably stronger curvature of parallels:
Compare Frančula XIII and Gott-Wagner.

And Another Note…

In my recent blog post regarding the political map images, I said that “sometimes a look at a political map is enough to discover the flaws of a given projection”. That I occurred to me when I rendered a map using the Anthracene projection, centered at 35° East, and looked at Myanmar:

But of course, it’s rarely that obvious…

References / Footnotes

↑ For more information about “Umbeziffern”, Wagner’s transformation method and the Böhm notation, read Das Umbeziffern – The Wagner Transformation Method, or the brief explanation in this blogpost or the notes at the Wagner Variations Generator (WVG-7).
↑ Sizing up the Universe by Gott & Vanderbei (2010)
Flat Maps that improve on the Winkel Tripel by Gott, Goldberg & Vanderbei (2021).
↑ More accurately, both Wagner IX and Gott-Wagner are modifications of the azimuthal equidistant projection, obtained by Umbeziffern.
↑ Goldberg & Gott, 2007:
Flexion and Skewness in Map Projections of the Earth
physics.drexel.edu/~goldberg/projections/goldberg_gott.pdf
↑ ix@60-52-450-38.5:
The second parameter actually is 90 / sqrt(3) [≈ 51,961524227066],
the fourth 200 / (3 × sqrt(3)) [≈ 38,490017945975].