Projective.

The blog of map-projections.net

• Show All
• News
• Articles
• Calendars
• → Go to Main Page

Fri Nov 26, 2021 Happy Birthday, Wagner VII!

Updated on Wed Mar 15, 2023

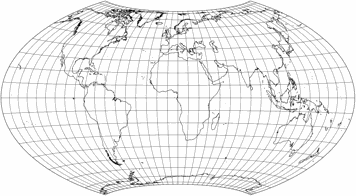
Eighty years ago, in 1941, Karlheinz Wagner the projection that nowadays is usually referred to as Wagner VII or Hammer-Wagner to the public.^[1]
Happy Birthday!

Wagner himself used none of the names given above. He simply *cough* called it “Flächentreuer Entwurf aus der transversalen flächentreuen Azimutalprojektion durch Umbeziffern entwickelt”, which roughly translates as “Equal-area projection, developed by Umbeziffern from the transversal azimuthal equal-area projection”. Maybe he noticed that this is a somewhat awkward name, so in 1949^[2] he switched to “Hammer’s projection with a pole line”.

It was introduced in an article titled Neue ökumenische Netzentwürfe für die kartographische Praxis – New Ecumenical Map Projections for Cartographic Practice –, and I have to elaborate on two things in this title:

1. What’s an ecumenical map projection?
Maybe you (just like I did) only know this word in a religious context. However the word ecumene also used to refer to “all inhabited areas of the world”.^[3] Think of thematic maps covering agricultural or economic topics or population density. Maybe also general-use or even political maps.

This is important to note because Wagner developed the projection specifically as an equal-area alternative to the Winkel Tripel which already was widely used at that time (at least, in Germany). And compared to this one, the Wagner VII of course squishes the polar areas extremely in North-South direction. But for the purposes mentioned above, it is (more or less) true that the accurate representation of these parts might be less important.

2. He talks about map projections. Plural.
So what are the other projections besides the Wagner VII?
Well, basically Wagner introduced just a single projection, but it can easily be customized in three ways:
– the length of the pole line,
– the curvature of the parallels,
– the aspect ratio of the main axes.

Wagner presented four projections variants using this approach, and a lot of other are possible – hence the plural.

The transformation method that is used to do this is called Umbeziffern (renumbering) but since I talked about this (and the Böhm notation which is a way to describe the resulting variants) more than once^[4], I won’t explain it again here…
Hey! Did I just hear a “Phew!” in the audience?!? 😉

Let me just briefly mention that the length of the pole line is given by a chosen parallel of the parent projection (the transversal azimuthal equal-area projection), which is referred to as ψ₁, while the curvature of parallels is determined by a meridian of the parent, λ₁.

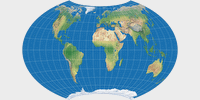
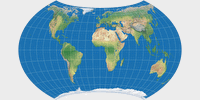
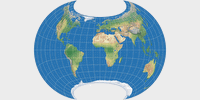
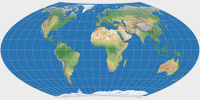
So here are the four variants presented in the paper – the first one being the one that nowadays is known as Wagner VII, the other three I’ve labelled VII.b, VII.c and VII.d. I’ll show them in a graphical representation that approximates Wagner’s original drawings (the caption states the Böhm notation, in which the first two figures note ψ₁ and λ₁, respectively):

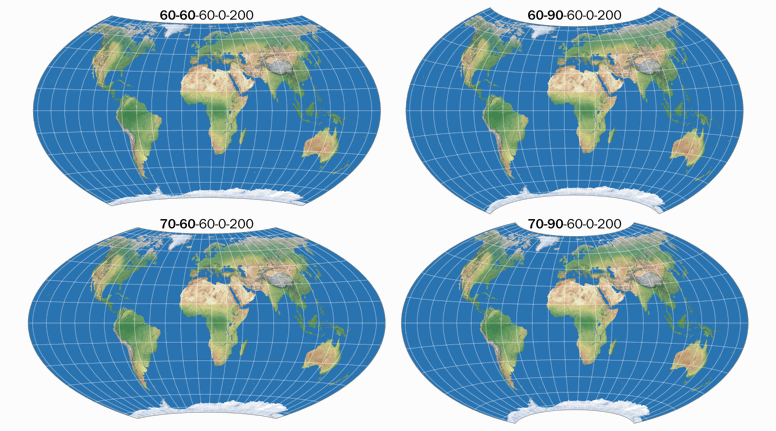
You will notice that the four variants do not differ that much. That’s because Wagner had a, well, strict notion about the acceptable range of the customizable values (at least for world maps). More specifically, he noted that the aspect ratio of the main axes should not move too far away from 1:2, and consequently, that the the most appropriate values for ψ₁ are to be found between 60° and 70°, and for λ₁ between 60° and 90°.

Let’s play with these values of the pole line length and the curvature of parallels. Preserving the aspect of 1:2, here are the four possible combinations of the minimum and maximum:

The pictures give an impression of the scope within which, according to Wagner, one arrives at a “good earth represenation”. We’ll see in a moment that other map makers have been less strict.

In his 1949 book “Kartographische Netzentwürfe”, Wagner took up the projection again - as already mentioned above, now under the name “Hammerscher Entwurf mit Pollinie” (Hammer’s projection with a pole line). There, however, he only showed the first of the four variants of his 1941 article. And while he certainly mentioned the approach’s possibilities for variation in the book, he unfortunately emphasised them less clearly. This is perhaps the reason why John P. Snyder also only mentions them “in passing” in 1993 – and the possible variety of forms was subsequently only taken up sporadically in the cartographic literature.

In the book, Wagner also adds a further way of modification, which is the possibility of adding a “prescribed areal inflation” which lead to compromise projections (like Wagner VIII). But since this is a blogpost about the 1941 jubilarian, I will refrain from a detailed discussion of the procedure at this point.
Although contradictorily, I will regard the Wagner VIII in the following section as well…

Usage of Wagner VII

The Wagner VII and his aphylactic brother VIII have been used in some German atlases and other publications. The ones that I know of are:

• The encyclopaedia Der neue Herder (1949) contains an inlay sheet showing a large political and three smaller thematic maps. The maps were drawn by Wagner himself and feature the Wagner VIII.^[5]
• The Columbus World Atlas of 1961 shows a physical, a political and a fistful of thematic maps using Wagner VIII. Hardly a surprise since this atlas was edited by – Karlheinz Wagner.^[6]
• No surprise either: The Atlas zur physischen Geografie, published 1971 by Karlheinz Wagner, shows a physical and an ocean map using Wagner VII, but in a further configuration. It’s not noted but the Böhm notation should be very close to 70-56-60-0-200. The ocean map is centered on 60° W and has some repetitions at the left and right edges.^[7][8]
  (Below you can see an approximating reconstruction of both maps.)
• Der große XENOS-Weltatlas used the Wagner VII for a political and a few thematic maps.^[9]
• Meyers großer Weltaltas (1997) used the above mentioned physical map of 1971 (more accurately: the same imagery, the type was set up again), and a political map using the same configuration.^[10]
• The Columbus Verlag (who used to publish the aforementioned atlas of the same name) offers wall maps using the Wagner VII projection.^[11]

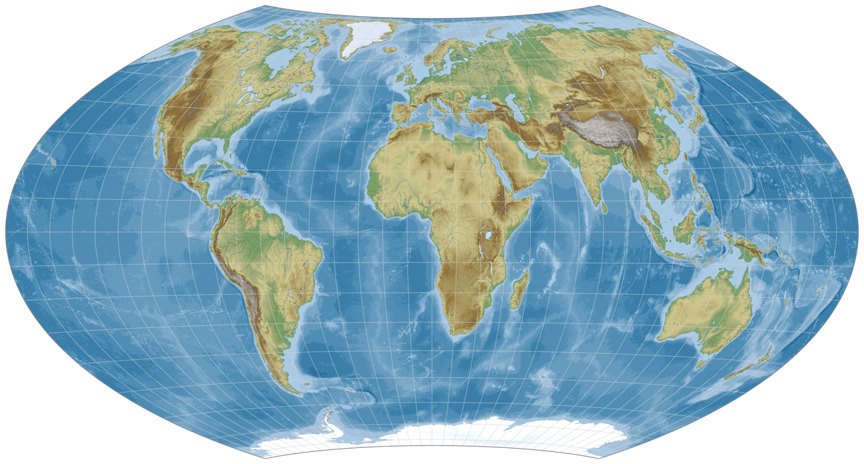
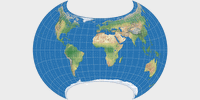
Wagner VII, as shown in the Atlas zur physischen Geografie and in Meyers großer Weltaltas.
The imagery presented here is somewhat alike, the configuration is either a very close approximation or identical.

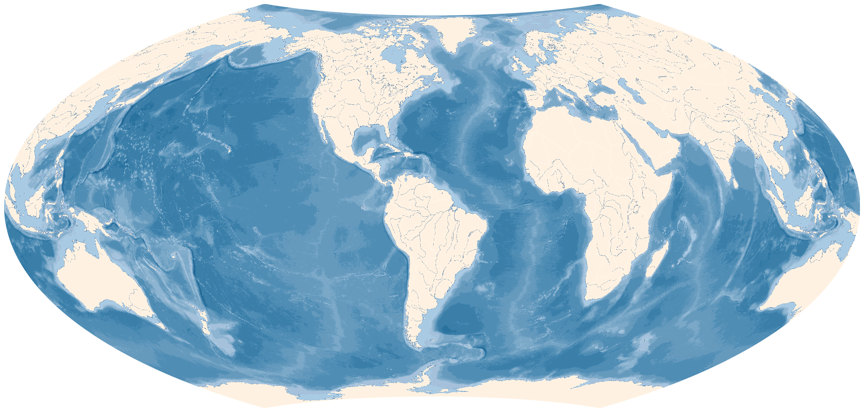
Wagner VII ocean map, as shown in the Atlas zur physischen Geografie.
Sorry about the crude reconstruction but at least it gives you an idea of what the map in the atlas is like.

The configuration 70-56-60-0-200 has now been added to my website. Continuing the naming scheme I applied to Wagner’s own variants, I called it Wagner VII.e. And yes, I know: There already are lots of Wagner variants there. However it would have felt wrong to list versions made by other creator, but to leave out an “original Wagner”.

Speaking of other creators…

Wagner VII variants by other creators

We’re back at equal-area projections only again, and take a quick look at Wagner VII variants made by other creators. The list includes two projections – Hammer and Eckert-Greifendorff – which were created prior to the Wagner VII but also can be written as its derivate.

As you can see, some of the creators were far less strict regarding the range of “acceptable” configuration values. But they had reasons to depart from them: Aribert Peters, Frančula^[12] and Canters^[13] used different metrics in order to achieve an optimization of distortion values. Dr. Böhm’s^[14] projections… well, I hope that sometime soon, I’ll at long last get around to say a few words about them as well. For the moment, you just have to take my word that he had reasons.

A “Birthday Present”

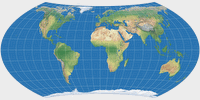
In order to celebrate the event, I’ve added another Wagner variant of my own to the website. It’s an asymmetric version of one of the 1941 projections, namely of the Wagner VII.b: The northern hemisphere is exactly the same, but by stretching the south pole line, the continental areas (except Antarctica) of the southern hemisphere are improved.

In an upcoming blogpost (hopefully soon) I’m going to say a few more words about the asymmetric Wagner VII.b – but for now, here it is:

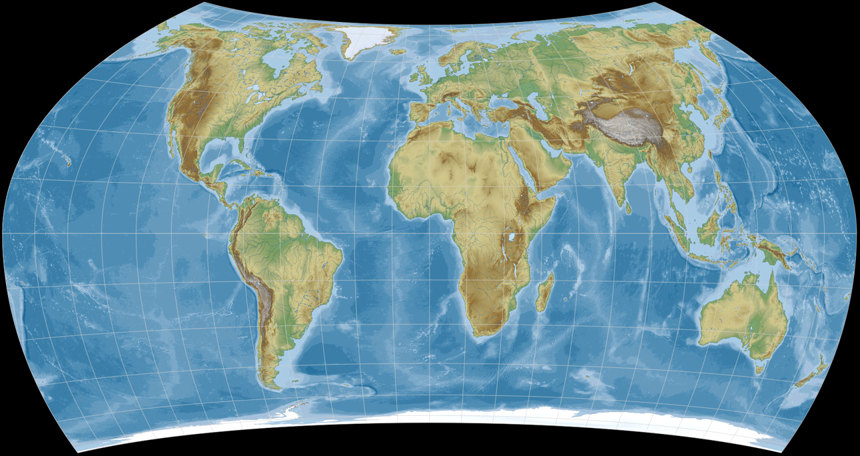
The asymmetric Wagner VII.b,
inspired by John G. Savard.

Closing Word

Apart from the set of different shapes shown here, you could also use the Wagner VII to create projections with straight parallels, i.e. pseudocylindricals. But basically, there’s no point in that – after all, there already are lots of pseudocylindric projections to choose from. And even if you want a customizable one, you might be better off with the Hufnagel projection.

Nonetheless, I daresay that whenever you need an equal-area world map, you’ll find a Wagner VII configuration that suits your needs. This of course doesn’t mean that there’s no other projection that’ll be just as good or even better for the purpose in question. You also have to remember that, despite it’s customizability, the Wagner VII can’t escape the basic characteristics of its parent projection’s graticule. You won’t be able to create projections like Strebe 1995 with its rounded corners, or Snyder Minimum Error Pointed-Pole and Hufnagel 10, which both have a pointed pole that looks like a pole line.

Wagner VII is one of my favourite equal-area map projections. This of course is a subjective choice, but I think you can’t deny that it’s one of the most useful map projections. And with the addition of the “prescribed areal inflation” eight years later it became even more useful.

HAPPY BIRTHDAY!

P.S.: The well-known variant of Wagner VII is offered by many map projection applications. G.Projector additionally offers a few other variants. The fully customizable Wagner VII/VIII is supported by Geocart and the d3-geo-projection scripts.
 
P.P.S.: This blogpost was modified on March 15, 2023, to reflect the new situation regarding the Columbus wall maps.

References / Footnotes

1. ↑ Wagner, Karlheinz:
   Neue ökumenische Netzentwürfe für die kartographische Praxis.
   In: E. Lehmann, ed., Jahrbuch der Kartographie 1941.
   Leipzig: Bibliographisches Institut. 176–202.
2. ↑ Wagner, Karlheinz:
   Kartographische Netzentwürfe.
   Leipzig 1949, page 225
3. ↑ see en.wiktionary.org/wiki/ecumene
4. ↑ For more information about Wagner’s transformation method, read this blogpost or the notes at the Wagner Variations Generator (WVG-7) or the article Das Umbeziffern – The Wagner Transformation Method.
5. ↑ Snyder, John P.: Flattening the Earth: Two Thousand Years of Map Projections.
   Chicago 1993, page 248.
6. ↑ Der neue Herder, Band II, M bis Z.
   Freiburg im Breisgau 1949.
7. ↑ Großer Columbus Weltatlas
   Neubearbeitet von Dr. Karlheinz Wagner.
   Columbus Verlag Paul Ostergaard KG / Kartographische Anstalt Dr. Wagner.
   Berlin/Stuttgart 1961.
8. ↑ Atlas zur physischen Geographie (Orographie)
   Herausgegeben von Dr. Karlheinz Wagner.
   Bibliographisches Institut AG, Geographisch-Kartographisches Institut Meyer
   Mannheim/Wien/Zürich 1971.
9. ↑ Der große XENOS-Weltatlas
   Hamburg 1996.
   German edition of the “International World Atlas”,
   Reed International Book Ltd., London (no year given).
10. ↑ Meyers Großer Weltatlas
    Herausgegeben vom Geographisch-Kartographischen Institut Meyer.
    Mannheim/Leipzig/Wien/Zürich:
    Meyers Lexikonverlag 1997.
11. ↑ Columbus Weltkarte
    Columbus Verlag Pauls Ostergaard GmbH.
    Currently (March 2023) there are three maps available: The German Weltkarte politisch-physisch and Weltkarte politisch-Satellitenbild; as well as the English The World Executive.
12. ↑ Nedjeljko Frančula: Die vorteilhaftesten Abbildungen in der Atlaskartographie (German).
    Also regard my blogpost The Frančula Projections.
13. ↑ Frank Canters:
    Small-scale Map Projection Design.
    London & New York 2002.
    Also regard my two-part blogpost The Canters Projections.
14. ↑ Dr. Rolf Böhm:
    Variationen von Weltkartennetzen der Wagner-Hammer-Aitoff-Entwurfsfamilie
    First publication in: Kartographische Nachrichten Nr. 1/2006. Kirschbaum: Bonn-Bad Godesberg.
    Als available at www.boehmwanderkarten.de/archiv/pdf/boehm_kn_2_2006_2015_complete.pdf (german)

Permalink

Comments

One comment

characters remaining: 2048

  

   Submit your comment   

Please leave the following four input field blank in any case!

Lutz

Hey Tobias, congrats to your impressive website(s) and blog(s). I just could not resist to comment here, because you updated this page on my birthday :-) (but I'm not Wagner VII)
I found your website(s) and blog(s) today by chance when I was looking for map projections that I maybe still could implement in my web tool http://www.lutanho.net/goodies/map2globe.html which I updated this week.
But after seeing that there are so many (I counted 355 on your website) and countless more by combining different parameters, this should surely be made in a separate tool.
How about an online tool on your website where users could load an image of a map (from harddrive or url), then choose the input projection, choose the output projection, set some sliders and then click "transform map projection" and it would create an image of the target projection in a canvas on the fly ready for download? The math shouldn't be the problem, also not the programing :-)

Thu Sep 19, 2024 11:52 am CEST   –    One Reply

Tobias Jung

Hello Lutz,
that’s a nice idea. I have thought about before, too, but I can see a few problems - not particularly big ones, admittedly, but big enough to make me think: »Oh, why bother? Why should I go through the trouble when in the end, ten people per year will user it?«

BUT … I’m not saying that I might not be convinced after all … ;-)
Kind regards
Tobias

Fri Sep 20, 2024 9:57 pm CEST

characters remaining: 2048

  

   Submit your Reply   

Please leave the following four input field blank in any case!

Go to top