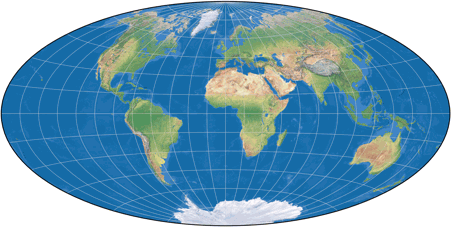
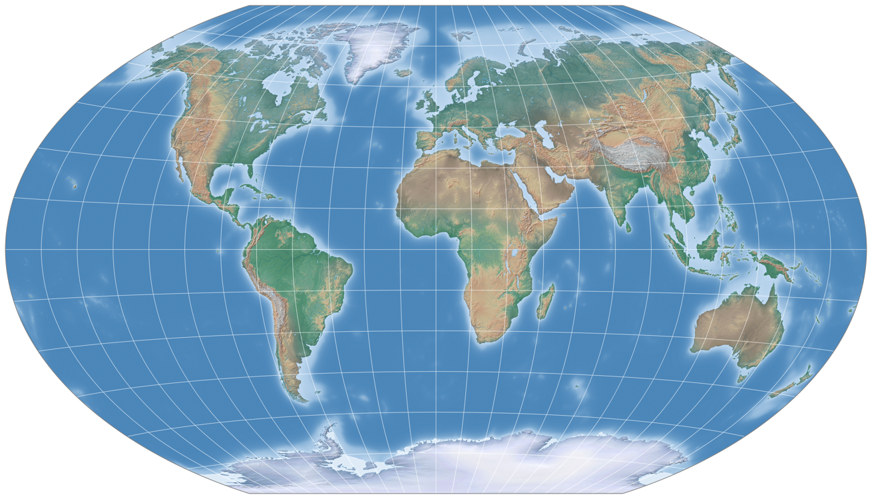
Thu Mar 18, 2021 Happy Birthday, Winkel Tripel!
A hundred years ago, in 1921, Oswald Winkel introduced his “Tripelprojektion”
– nowadays usually referred to as Winkel Tripel or sometimes
Winkel III – to the public.[1]
Happy Birthday!
The paper was published in the December issue of Petermanns Mitteilungen, so maybe the congratulations would have been more appropriate later this year. But on the other hand, the original illustration is subscribed with the remark: Drawn for the first time on September 15, 1920. So that was the actual birthday…
The Winkel Tripel used to be my favorite projection back when I knew only a fistful of projections (being, besides the jubilarian, the Mollweide, van der Grinten I, Gall-Peters and of course the Mercator projection). Well, meanwhile, I know a few projections more 😉 and there are others that I prefer, but I still like the Winkel Tripel a lot. More importantly, there’s no denying that it’s an absolutely remarkable projection.
Before we come to the remarkable part, let me repeat a few words that I’ve said before:
Oswald Winkel designed the Winkel Tripel by calculating the arithmetic mean of
the Equirectangular and the Aitoff projections.
On the Equirectangular you can set the standard parallels, and Winkel chose approx. 50°28´ –
that’s arccos(2/π) to the mathematicians[2] –
before mixing it with the Aitoff.
The Aitoff projection…
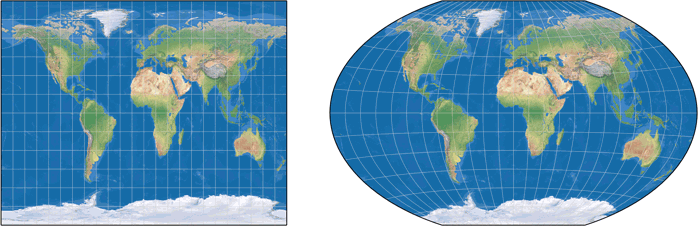
… arithmetically averaged with Equirectangular, standard parallels at approx 50°28´,
results in the original Winkel Tripel.
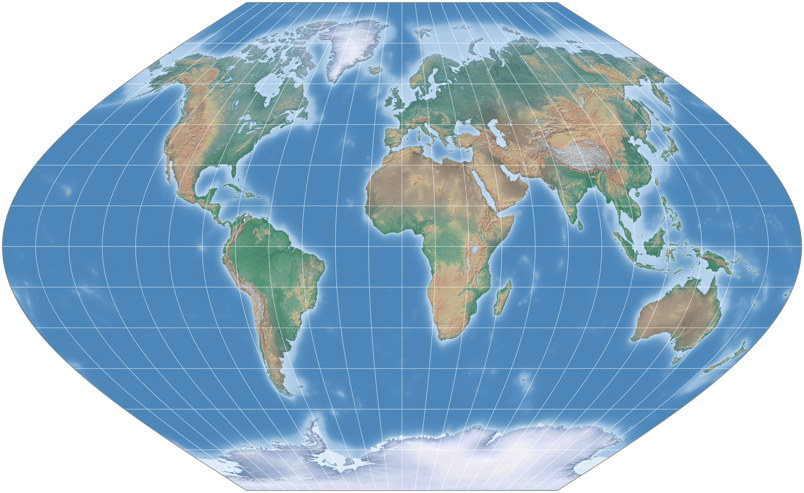
About 1955, John Bartholomew designed a Winkel Tripel variant for the Times Atlas, in which he chose 40° as
standard parallels for the Equirectangular portion of the projection. The resulting projection is wider
than the original and many people will argue (and I agree with them) that it shows a better distribution
of distortions. By the way, Karlheinz Wagner pointed out already in 1949, that this value
»seems to be the most appropriate for a world map« and presented a corresponding figure.[3]
Here in this website, this variant is filed under »Winkel Tripel Bartholomew«.
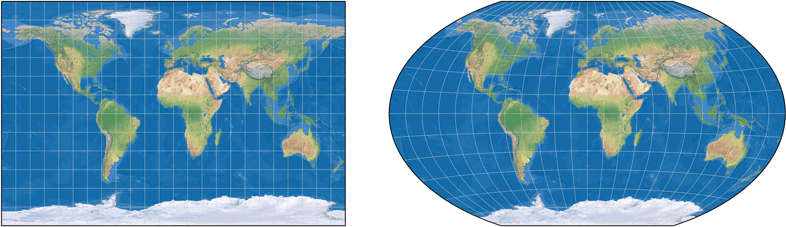
Setting standard parallels to 40° on the Equirectangular portion will give you Winkel Tripel Bartholomew.
Here it is again larger:
The Winkel Tripel became extremely popular comparatively quickly – at least in the German-speaking countries. In 1941, Wagner noted that it could be seen “in a wide variety of new map works by almost all authoritative companies” and praised “its amazing fidelity of form and position. One could think that Winkel had carefully smoothed the doubly curved surface of the sphere, always careful not to force the individual parts in a certain direction, but yielding a little on all sides, in order to finally obtain a representation that is as similar as possible [to the representation on the globe] in every respect”.[4] [5]
As a side note, Wagner VII (which I like a lot) was explicitly introduced by its creator as an equal-area alternative to Winkel Tripel. So without Winkel’s projection, perhaps there would be no Wagner VII at all…
Of course there’s not only praise. Even Wagner, who usually refers to the projection with such
kind words as those quoted above, smuggled in a cautious criticism:
“However, the increase in area from the equator to the pole is quite considerable.”[6]
Eckert begins with half-hearted kind words to then criticize its nature of being an aphylactic projection:[7]
Asked for my opinion about Winkel’s projection, I have to say that I, too, like it quite well and consider it quite suitable for general-use maps. However, I myself, carried by a healthy geographical and mathematical consciousness, prefer the projections that have a stable mathematical foundation and are either equivalent or conformal or equidistant (…)
Herbert Hufnagel points out the unfavorable distribution of distortions:[8]
The area inflation continuously increases from the equator to the poles (…) but the area also changes with increasing distance from the central meridian. However, the increase from the equator to the poles is different depending on the distance of the meridian from the map center. The result is that on the equator the area increases from the map center towards the boundaries, but on the parallels of latitude beyond about 50° N/S it decreases. This phenomenon is the result of mixing two projections with very different characteristics; it makes it impossible to take the increase in area into account when making comparisons.
… and concludes, that projections with “controlled areal inflation” in the manner of Wagner VIII
should be preferred.
Hey! That makes my own Wagner BCW-A and
F13 Copycat
recommendable alternatives to the Winkel Tripel! I love this critique!
😁😉
Okay, jesting aside:
Except for the usage in the Times Atlas, the Winkel Tripel remained
“almost unknown” in non-German speaking countries – at least,
according to Hufnagel.[9] This changed in 1998, when the National Geographic Society adopted
the original version as standard projection for world maps.
And nowadays, as far as I can tell it’s one of the most frequently used projections worldwide.
And nor, for the remarkable part …
First off, it’s noteworthy that the Winkel Tripel was the first pole line projection in the group for which I have adopted the term lenticular[10] (while others prefer polyconic, pseudoazimuthal etc.) – but this is not the really remarkable thing.
I’ve said it time and again that I suck at math.
So maybe I’m getting something wrong, but –
mixing two existing projections seems quite trivial to me,
especially when I look at the formulae of newer projections,
e.g. the ones developed by Canters or Györffy.
And yet …
- The Winkel Tripel Bartholomew took the pole position in Canters’ list of 23 well-known projections sorted by the mean finite scale factor K1; [11] (regrettably, the original version wasn’t mentioned here)
- rank 1 (original) and 2 (Bartholomew) in Goldberg’s and Gott’s (2007) list of 6 projections “with the lowest values of ∑ε”; [12]
- the same ranks in Frančula’s (1971) list of 10 frequently used projections, sorted by the Airy-Kavraiskiy criterion EAK; [13]
- rank 2 for the Bartholomew version in Györffy’s list of the related EK value for well-known 18 projections (again, the original isn’t listed); [14]
-
and rank 9 (Bartholomew) and 12 (original) in a list of 100 projections sorted by
Richard Capek’s distortion characterization Q in 2001 [15]…
Ooops, what happened here? Well, apart from the fact that I have come to doubt the usefulness of Q a bit (which is sad because it’s the most extensive study), they score 81.3 and 80.7 points, which still is very good, despite the seemingly “bad” ranking.
Of course, the studies by Canters, Goldberg & Gott, Frančula and Györffy were not what I’d call extensive. For example, none of them evaluated Ginzburg VII (1950) or Ginzburg IX (1966), and just a few days ago, I learned that both beat the Winkel Tripel according to the Airy-Kavraiskiy criterion and the Goldberg-Gott metric. Even among my own experiments are two – the F13 Copycat and the Wagner BCW A III –, which pull ahead of the jubilarian.[16] So it’s quite possible that there are other projections that outperform the Winkel Tripel. But I think there can be no doubt that it presents a very beneficial balance of angular deformation and areal inflations.
There can also be no doubt that the Winkel Tripel has been
outperformed a number of times since the age of “computer-aided map projection design” started:
By projections created by Frančula, Canters,
Györffy, probably by Kunimune[17]…
But the thing about these is: They used computers to optimize projections.
They calculated a large number of configurations
until they arrived at the most favourable distortion values possible.
Their projections were created at considerable computational expense.
So, do you need computational power to beat the Winkel Tripel? – No.
But most projections that are better, were created by an optimization process.
So one can say: It’s not impossible to beat the Winkel Tripel
– but it’s surely not easy.
And that you can say this about a projection that simply was created by the arithmetic mean of two other projections – I think that is remarkable indeed.
Note: When I talk about “being better than” or “beating” etc. a given projection, you should always add “according to a specific usage of a specific comparison scheme” in your mind. There is no final solution to compare the overall distortion of different projections. Is there a standard solution at least? – No. The current state of affairs is much like it is depicted in the wonderful xkcd “Standards” cartoon.
… and Happy Birthday, Winkel I and II!
Winkel I and II are mixed projections, too. The first parent projection is,
just like on the Tripel, the equirectangular projection with standard parallels at arccos(2/π),
the second parent is
the sinusoidal projection
for the Winkel I and the
Apian II
on the Winkel II.
They were devised earlier, namely in 1914 and 1918, but to my knowledge introduced to the public in the
same paper as the Winkel Tripel.
They are far less famous than the Winkel Tripel, although in my opinion, the Winkel II is a very nice, usable projection with straight, equally spaced parallels – and recently, I have been told that among the pseudocylindrical projections it’s as hard to beat as it’s lenticular brother.
As for the Winkel I, well…
I’ve said it before, projections with sinusoidal meridians
do not seem to be favoured by a lot of people. Personally, I don’t
even find it unattractive, but on the other hand, I also can’t think
of any purpose for which it would be my first choice.
However: Happy Birthday to Winkel I and II, too!
References / Footnotes
-
↑
Winkel, Oswald: Neue Gradnetzkombinationen. In: Petermanns Mitteilungen. 67, 1921, 248–252.
Englische Übersetzung (inkl. Illustrationen) verfügbar untercsiss.org/map-projections/microcam/newgrat.pdf
Scan des deutschen Original-Artikels (keine Illustrationen, schlechte Qualität) untercsiss.org/map-projections/microcam/winkel.pdf
Update 5.5.2022: Sorry, die vorgenannten Links funktionieren nicht mehr. 😕 -
↑
arccos(2/π) is not exactly 50°28´, but – in case I didn’t miscalculate this –
50,45977625219° or 50°27´35.1945″. But you can safely disregard this: On a printed map, the difference is probably
less than the warpage of the paper the map is printed on.
And in an digital image having a width of about 12,000 pixels the maximum difference is two pixels. (And yes, I was crazy enough to try…) -
↑
Wagner, Karlheinz:
Kartographische Netzentwürfe.
Leipzig 1949, page 225 -
↑
Wagner, Karlheinz:
Neue ökumenische Netzentwürfe für die kartographische Praxis.
In: E. Lehmann, ed., Jahrbuch der Kartographie 1941.
Leipzig: Bibliographisches Institut. 176–202. - ↑ The translation of the longer quote knocked me out so I relied on the translation that www.DeepL.com/Translator (free version) gave me. In case you’re interested, here are Wagner’s original words: He praised “seine verblüffende Formen- und Lagetreue. Man könnte meinen, Winkel habe behutsam die zweifach gekrümmte Kugeloberfläche geglättet, immer bedacht, die einzelnen Teile nicht gewaltsam in eine bestimmte Richtung zu zwingen, sondern nach allen Seiten ein wenig nachgebend, um schließlich ein in jeder Hinsicht möglichst ähnliches Abbild zu bekommen.”
- ↑ Wagner 1949:226
-
↑
Eckert-Greifendorf, Max:
Kartographie. Ihre Aufgaben und Bedeutung für die Kultur und Gegenwart
Berlin 1939, page 75f. -
↑
Hufnagel, Herbert:
Die Verwendung von Kartennetzen.
In: Kartographisches Taschenbuch 1988/89.
Bonn 1988. 11–20. -
↑
Hufnagel, Herbert:
Ein System unecht-zylindrischer Kartennetze für Erdkarten.
In: Kartographische Nachrichten 39/3: 89-96; München Juni 1989. - ↑ see Strebe, Daniel “daan”: Map Projection Essentials
-
↑
Frank Canters:
Small-scale Map Projection Design.
London & New York 2002. -
↑
Goldberg & Gott, 2007:
Flexion and Skewness in Map Projections of the Earth
physics.drexel.edu/~goldberg/projections/goldberg_gott.pdf - ↑ Nedjeljko Frančula: Die vorteilhaftesten Abbildungen in der Atlaskartographie (German)
-
↑
János Györffy, 2018: Minimum distortion pointed-polar projections for world maps by applying graticule transformation
doi.org/10.1080/23729333.2018.1455263 -
↑
Richard Capek, 2001:
Which is the Best Projection for the World Map?
icaci.org/files/documents/ICC_proceedings/ICC2001/icc2001/file/f24014.pdf - ↑ The F13 Copycat was introduced in the blogpost The Frančula Projections, the Wagner vii@65-76-60-40-168 in Two new projections, three variants, some adjustments.
- ↑ Justin Kunimume 2019: Introducing the Danseiji Projections
P.S.: And Happy Birthday to you, too, K.J.! 😁

 Except where otherwise noted, images on this site are licensed under
Except where otherwise noted, images on this site are licensed under
Comments
Be the first one to write a comment!