Wed Jan 01, 2020 Two new projections, three variants, some adjustments
At the beginning of 2020, I’d like to publish a little update.
So, here are two new projections, three new variants – and a few
adjustments.
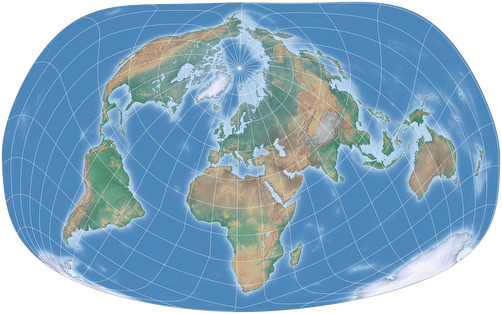
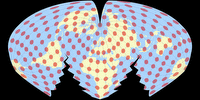
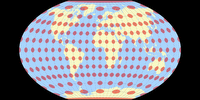
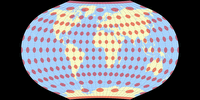
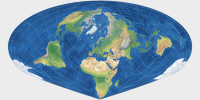
The Bertin-Rivière projection
Based on a 1953 drawing by Jacques Bertin, which most likely was not created using a mathematical formula,
Philippe Rivière created this new projection in 2017.[1]
… Well, I am calling this a new projection, because in my opinion it differs
too much from the original to be called Bertin projection.
So I’m using the name that is also used by the software G.Projector:
Bertin-Rivière.
Mathematically, it was built using the Briesemeister projection[2], which itself was derived from the Hammer projection – so, hey, maybe I should call it the Hammer-Briesemeister-Bertin-Rivière projection? 😉 Naaah…
However, it is an interesting projection that keeps the distortions of the land masses low. Enjoy:
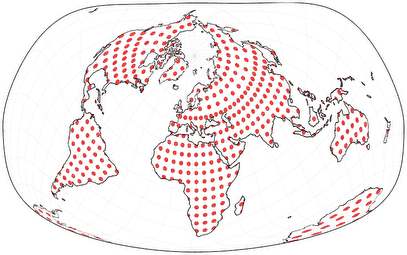
And to emphasize the specific distribution of distortions, here’s an image with the Tissot indicatrix displayed on land masses only (the usual Tissot rendition is of course available at the list on the website).
And here’s the usual image of the Tissot indicatrix, along with the mathematical parent projection Briesemeister, and both the interrupted and uninterrupted version of Sinu-Mollweide which is a bit similar.
Bertin-Rivière vs. Briesemeister
Bertin-Rivière vs. Sinu-Mollweide
Bertin-Rivière vs. Sinu-Mollweide (uninterrupted)
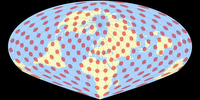
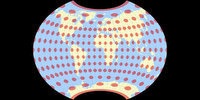
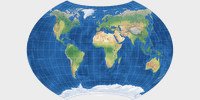
Györffy E
In 2018, János Györffy introduced a series of five minimum error projections[3], labelled
A, B, D, E and F (C was discarded because there was no notable difference towards B).[4] His goal was to reduce both angular and areal distortions on aphylactic (compromise) pointed-pole projections with an outer shape
that will »remind the viewer of the Globe«.
A and B are pseudocylindricals while D, E and F belong the class of lenticular projections.
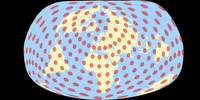
Regrettably, I can show but one projection out of this series, namely the Györffy E:
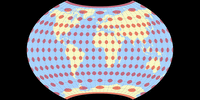
Let’s compare it to the Tissot indicatrix of some similar projections… ooops! There aren’t any!
Except for the Aitoff (which really doesn’t look similar), there are no lenticular pointed-pole compromise projections! So, let’s
do the next best thing and compare it to some lenticular compromise projections with a pole line – there’s a bunch of them,
so I selected a few having areal distortions which are roughly in the ballpark of Györffy E’s distortion values. Very roughly.
You also can compare the Györffy E directly to the six other projections using the following links…
(Note: The links trigger the Expert Mode of the comparison. For these pairings, it’s
advisable to scroll down to the “scaled to same width” examples.)
Györffy E vs. Kramer VII
Györffy E vs. Winkel Tripel
Györffy E vs. Ginzburg V
Györffy E vs. Wagner IX.i
Györffy E vs. Wagner IX, Canters’ optimization
Györffy E vs. Wagner vii@65-76-60-40-168
Three new variants
Also, I’ve added three variants of projections that already have been on this website for some time…
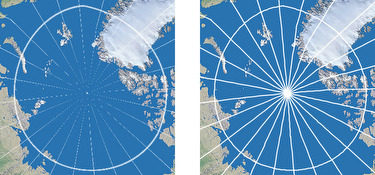
The equirectangular projection is already listed in two variants, one using the
equator as standard parallel (= plate carrée projection) and the other other one with
standard parallels at 35.6° N/S.
You’ll read below why I felt obliged to add another variant, this time with
standard parallels at 28° N/S.
The uninterrupted variant of Philbrick Sinu-Mollweide. You’ve already seen it above – I have to admit, I can’t remeber why I neglected to add it the day I added the interrupted version.
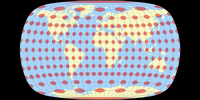
Hey, a Wagner variant! I don’t think you’ve seen one before! 😉
This variant (already shown above, too) is somewhere in between the Wagner BCW-A I
and Canters optimization of Wagner IX. The Böhm notation[5] is Wagner vii@65-76-60-40-168, and for the lack
of creativity, I’m using this as the projection’s name
since March 26, 2021,
it’s called Wagner BCW-A III.
There’s nothing special about this Wagner variant, I just… well, liked it.
To create this projection in Geocart,
choose the generalized Wagner with following parameters:
a = 2.16538, b = 1.4769, m = 0.975032, m2 = 0.75955, n = 0.422222
In d3-geo-projection, use:
d3.geoWagner().poleline(65).parallels(76).inflation(40).ratio(168)
Lets have a glance at the distortion characteristics and then move on:
Adjustments
More than four years ago, I added the Patterson cylindrical projection – but the images I presented were wrong! 😱
There was a flaw in the map projection software I used for the Patterson images
(G.Projector)
so it was rendered with an width-to-height ratio of roughly 0.61
instead of 0.57 as specified.
The flawed images were replaced by correct renditions.
Current versions of G.Projector create a correct Patterson as well.
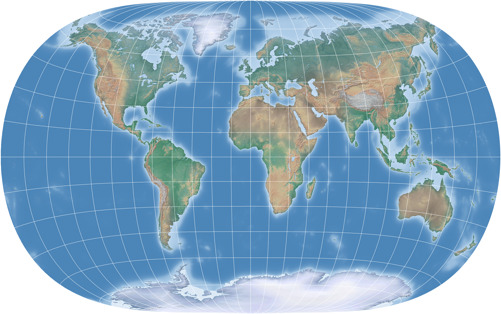
And while I was at it, I replaced the topographic map in
the Patterson article
with a new one that I like much better.
🌐
The next adjustment can be handled in a single sentence: Images of the Dymaxion projection had broken graticule lines – thanks to a new version of Justin Kunimune’s map projection software, this is fixed.
🌐
Two years ago I began to use new images for the Tissot indicatrix, but only for projections that were added thereafter. Now, I replaced some of the older Tissot images with the new version. Namely all that were shown above (Winkel Tripel, Ginzburg V, …).
Footnotes
-
↑
Philippe Rivière: Bertin Projection (1953)
visionscarto.net/bertin-projection-1953 -
↑
Demonstrating the transformation of the Briesemeister to get the Bertin-Rivière projection:
bl.ocks.org/Fil/5b9ee9636dfb6ffa53443c9006beb642 -
↑
János Györffy: Minimum distortion pointed-polar projections for world maps by applying graticule transformation
doi.org/10.1080/23729333.2018.1455263 - ↑ Györffy uses lowercase letters to label his projections, but I found uppercase letters to me more legible.
-
↑
Wagner’s Umbeziffern and the Böhm notation:
map-projections.net/wagner-umbeziffern.php
Comments
One comment
Peter Denner
What's the reason why you can only show Györffy E?
It's occurred to me that Györffy B (and the almost identical Györffy C) might be very similar to Winkel II, but while Györffy B and C required the numerical optimization of 3 and 4 parameters, respectively, Winkel made his projections by setting just one parameter (the standard parallel of the equirectangular projection that they're partly derived from), and all without the help of a computer!
Yes, Winkel II has a pole line, but Györffy B, C and E are so flat at the poles that they might as well have a pole line too.
Obviously, your website would offer the best way of comparing Györffy B (and/or C) and Winkel II, if only the other Györffy projections were on here.
I presume the reason is that Györffy E is the only variant available in the software packages that you use to create your images. What software packages are these, and do any of them have the possibility of entering the formula for a projection yourself? Could you get good enough images from d3?






 Except where otherwise noted, images on this site are licensed under
Except where otherwise noted, images on this site are licensed under
Tobias Jung
thanks for your comment!
> I presume the reason is that Györffy E is the only variant available in the
> software packages that you use to create your images.
Exactly!
> What software packages are these
Geocart, G.Projector, Flex Projector, MapDesignerRaster and d3-geo-projection.
> and do any of them have the possibility of entering the formula for
> a projection yourself?
No. Well, at least not as a part of the GUI – the d3 scripts allow (as you know, but maybe not the other readers) to add own functions rendering new projections.
> Could you get good enough images from d3?
Yes, at least good enough for the use on the web. But this only works if the formulae include the inverse function. Moreover, using images from d3 is always a bit of work in post-processing…
Kind regards,
Tobias
Peter Denner
No pressure – feel free to say no.
Tobias Jung