Fri Jan 05, 2024 The Winkel-Denner Projections
Updated on Mon Jan 15, 2024
A while ago, I mentioned that there is “another good thing about the Winkel-Snyder”. And that is that it kind of triggered the creation of five very interesting projections by Peter Denner – and two, hopefully also not too bad, by myself.
Peter introduced his projections in April in a thread of the mapthematics forum. I’ll mostly just quote here what he said there, but since I’ll also present the distortion plots (once more provided by Peter), it may be worthwhile to read this blogpost even if you’ve already read that thread.
Before I start, I have to say something that, strangely enough, I have never mentioned before,
although it would fit well in the
basic knowledge section of my website:
We will be talking about x and y values here. And yes, that’s referring to exactly
that thing that you (hopefully) remember from your geometry lessons in school.
That’s what map projections are all about: Transferring spherical polar coordinates to
coordinates you can draw in a cartesian coordinate system.
Let’s get it started – and, der Esel nennt sich immer zuerst, I’m going to begin with one my own projections.
Winkelish Projection I
In a a comment in February, Peter Denner mentioned the Winkel-Snyder. We continued to talk about this projection, and during the conversation, I remembered an experiment of my own that I carried out in August 2018 and showed it to Peter. I was an attempt to create a “Winkel-Tripelish” projection with lower areal distortion (knowingly at the expense of higher angular distortion).
The idea was easy: Winkel Tripel’s x and y values are the arithmetic means of the equirectangular and Aitoff projections. So it’s obvious that you can reduce the areal inflation if you replace the Aitoff with the equivalent Hammer projection. I tried this with standard parallels at arccos(2/π) (≈50°28´, or 50.46°, resulting in the same aspect ratio like Winkels original) and 40° (aspect ratio like the Winkel Tripel Bartholomew). Here are the results – in both cases the Hammer is scaled up to the size of the Aitoff before averaging with the equirectangular:
Compare:
Winkelish Projection I (50.46°) vs. Winkel Tripel
Winkelish Projection I (40°) vs. Winkel Tripel Bartholomew
Winkelish Projection I (50.46°) vs. Winkelish Projection I (40°)
I have to say that I was not very fond of this projection (and I still not am),
that‘s why I discarded it at that time. Now I am adding it to my Projection Collection for
three reasons:
1. While it’s not great, it’s certainly not bad;
2. a large part of this website is about comparing map projections,
showing their advantages and deficiencies,
so even projections
that are not that great have its place;
2. it makes a good intro for the Winkel-Denner projections.
Because where I just said: “Oh, this does not look very good” and then left it at that, Peter tried to figure out why this is the case.
Winkel-Denner I
or
Winkel Tripel lower areal distortion
So, when Peter asked himself why the Winkelish I didn’t look that great …
Oh well. I’m going to be lazy and simple quote his words from the forum thread mentioned above:
I was wondering why this might be and thought that maybe it was because the spacing of the meridians is also modified, with everything getting pushed outwards to regions of higher distortion and the Americas in particular looking rather bent.
It occurred to me that you could modify the spacing of the parallels in the Winkel Tripel without changing the spacing of the meridians if you stick with Winkel's average of the equirectangular and Aitoff projections for the x values but take the average of the equirectangular and (scaled up) Hammer projections for the y values.
I’ll keep quoting Peter throughout this blogpost, without explicitly mentioning it. Whenever you see a paragraph that looks like the one above, you know that these are not my own words but Peter’s. Here are his first results, again with the standard parallels at arccos(2/π) and 40° (another thing that I will keep up for the rest of this blogpost):
Compare:
Winkel-Denner I (50.46°) vs. Winkel Tripel
Winkel-Denner I (40°) vs. Winkel Tripel Bartholomew
Winkel-Denner I (50.46°) vs. Winkel-Denner I (40°)
Like the Winkelish I, the Winkel-Denner I has lower areal distortion at the expense of higher angular distortion, but Peter concluded (and I agree) that overall, his projection is better.
Winkel-Denner II
or
Winkel Tripel lower angular distortion
Apparently, that raised Peter’s eagerness to experiment, and he continued:
You can of course also shift the parallels of the Winkel Tripel in the other direction such that they’re closer together near the equator and further apart near the poles. At first glance, you might think that taking the average of the equirectangular projection and the Aitoff-transformed[1] stereographic projection for the y values would be a good choice. However, the spacing of the parallels deviates from equidistance by a much greater amount in the stereographic than in the azimuthal equal-area, from which the Hammer is derived, so this results in a much greater modification of the spacing of the parallels than in projection 1.
So Peter Denner simply created a new azimuthal projection, took the average of the equirectangular and Aitoff projections for the x values and the average of the equirectangular projection and the Aitoff-transformed version of this new azimuthal projection for the y values, and presto! There’s the Winkel-Denner II which, compared to the original Winkel Tripel, has lower angular distortion at the expense of higher areal distortion:
Compare:
Winkel-Denner II (50.46°) vs. Winkel Tripel
Winkel-Denner II (40°) vs. Winkel Tripel Bartholomew
Winkel-Denner II (50.46°) vs. Winkel-Denner II (40°)
So far, all three projections are (purposely) very similar to the original Winkel-Tripel. Most people, myself included, would probably think it is the original, if they’d see them printed in an atlas or on a wall map. The next ones look somewhat different.
Winkel-Denner III
or
Winkel Tripel rounded corners
The whole reason for averaging a pointed-pole parent projection with the equirectangular projection in the first place is to introduce a pole line. However, once you accept that you don’t have to use the same parent projection for the y values that you use for the x values, it becomes apparent that you don’t need to take the average with the equirectangular projection at all for the y values and you’ll still have the same pole line. Taking the average of the equirectangular and Aitoff projections for the x values and just taking the Aitoff projection alone without any averaging for the y values gives a projection that’s essentially the Winkel Tripel but with rounded corners:
Compare:
Winkel-Denner III (50.46°) vs. Winkel Tripel
Winkel-Denner III (40°) vs. Winkel Tripel Bartholomew
Winkel-Denner III (50.46°) vs. Winkel-Denner III (40°)
I have to say that I’m not really sure about the “essentially the Winkel Tripel” bit – although it is almost identical in the center of the map. The outer shape, though, is more similar to Winkel’s second projection; so maybe you could also call this projection also the Lenticular Winkel II. 😉
Winkel-Denner IV
or
Winkel Tripel rounded corners lower areal distortion
The obvious next step is now to replace the Aitoff with the Hammer and with the Aitoff-transformed new azimuthal projection introduced [above], as in projections 1 and 2 respectively, in order to modify the spacing of the parallels in this new version of the Winkel Tripel with rounded corners. However, in projections 1 and 2, the spacing of the parallels is tempered by averaging with the equirectangular, so if we just take the Hammer projection or the Aitoff-transformed new azimuthal projection alone without any averaging for the y values, then the parallels in the resulting projection will deviate from being equally spaced by a greater amount than in projections 1 and 2. Of course, this doesn’t mean that you can’t do it, (…) but personally, I don’t like parallels that deviate too much from being equally spaced in compromise projections. (…)
So instead of taking the Hammer projection or the Aitoff-transformed new azimuthal projection alone without any averaging for the y values, we first take the average of the Aitoff and (scaled up) Hammer projections for the y values:
Compare:
Winkel-Denner IV (50.46°) vs. Winkel Tripel
Winkel-Denner IV (40°) vs. Winkel Tripel Bartholomew
Winkel-Denner IV (50.46°) vs. Winkel-Denner IV (40°)
And we go directly to the fifth projection …
Winkel-Denner V
or
Winkel Tripel rounded corners lower angular distortion
… which is the average of the Aitoff projection and the (scaled down) Aitoff-transformed new azimuthal projection for the y values:
Compare:
Winkel-Denner V (50.46°) vs. Winkel Tripel
Winkel-Denner V (40°) vs. Winkel Tripel Bartholomew
Winkel-Denner V (50.46°) vs. Winkel-Denner V (40°)
Projections IV and V have significantly lower overall angular distortion and approximately the same overall areal distortion as their counterparts with pointed corners, Winkel-Denner I and II.
I’ll save the résumé for later. Before that, I’d like to show another one of my own experiments.
Winkelish Projection II
Note from January 15th:
The Winkelish Projection II was revised after the original presentation on January 5.
As I said above, I wasn’t very satisfied with the Winkelish Projection I, but
I still was eager to see a Winkel Tripel with lower areal inflations
(the Winkel-Denner projections didn’t exist at that time).
So I wanted to try it the other way round: Instead of replacing the Aitoff with a projection that has
lower areal inflations, I could replace the equirectangular projection!
So I averaged the Aitoff with the cylindric equal-area projection but that didn’t look “winkelish”
at all. Well, then, just take a cylindric projection that has some amount of areal inflation but
as much as the equirectangular, and that would be, ummmm, … Oops!
Indeed, I couldn’t find a single named cylindric projection that matches this description.[2] So I decided to use the customizable Wagner VII/VIII: If you set both the bounding parallel ψ1 and the bounding meridian λ1 to 0 (zero), you’ll get a cylindric projection (see this example in my Wagner Variations Generator). Then, apply an amount of areal inflation of your choice. I decided on 1.5 at 60° N/S, which is halfway between the cylindric equal-area and the equirectangular projection.
In the first version of Winkelish II (published on Jan 5) I set
the desired aspect ratio using the variable p (as usual on the generalized Wagner)
and mixed it with the Aitoff projection without prior scaling.
Peter Denner then proposed a slightly different version having two improvements:
– Just like the projections above, it includes rescaling so the projection
fits in with the rest of the series because of matching pole line lengths,
– the aspect ratio of the cylindrical portion is set by giving the
standard parallel, which is common practice for (pseudo)cylindricals
and allows to draw the Winkelish II with exactly the same
aspect ratio as the Winkel Tripels.
Compare:
Winkelish Projection II (50,46°) vs. Winkel Tripel
Winkelish Projection II (40°) vs. Winkel Tripel Bartholomew
Winkelish Projection II (50,46°) vs. Winkelish Projection II (40°)
Résumé
We’ve seen seven alternatives to Winkel Tripel. My first winkelis projections and
Winkel-Denner I & II are very close to the originals by
Oswald Winkel and John Bartholomew, with certain advantages, which come at
the cost of certain disadvantages.
Winkel-Denner III, IV & V are visually more distinctive,
and my second winkelish projection is somewhere in between.
Because of that, and because the improve on the overall distortion (see below),
I think this three projections by Peter Denner are the most
interesting ones in the line-up I showed here.
The good compromising properties of the original are retained,
the rounded corners may appear more pleasing to many eyes
and prevent confusion with the Winkel Tripel.
I wouldn’t go so far as to say that the Winkel Tripel is overused. But it surely is used very
often, so it can’t hurt to resort to other projections from time to time.
Winkel-Denner III, IV & V are, in my opinion, very good choices for atlases,
wall maps, and many kinds of thematic maps.
My personal favorites are Winkel-Denner I
(for “the almost identical to Winkel Tripel” projections)
and Winkel-Denner IV (for the novelty projections).
How To Use the Projections
Now for the bad news: Currently, the only software that can render the projections shown here (except for the Winkelish II, see below) are d3-geo-projection scripts, and they are great for vector graphic maps and, as you can see, also for also for web-suitable images – but less so for graphics that are to be printed.
The good news… well, the formulae for the projections are nothing fancy, quite basic math. It should be too hard to integrate them into map projection applications. Which of course does not necessarily mean that it’ll happen. 😕
Six of the projections above use a scaling before averaging – this process
isn’t supported by the application
Geocart.
The only exception is the Winkelish Projection II
where you can use the projection parameters to perform the rescaling.
So, in Geocart you can first create a map using the Aitoff projection,
then one using the “generalized Wagner” using following parameters
for the 50,46° version:
a = 2001.949, b = 1571.3114, m = 0.001131, m2 = 0.69016, n = 0.000318
Or these for 40°:
a = 2408.9448, b = 1571.3114, m = 0.001131, m2 = 0.69016, n = 0.000318.
Then, select both maps, choose Map → New Blended from the menu, and mix
the maps with P = 0.5.
To render the seven projections using d3, download the following file –
but please note that this is not a standalone, ready-to-use file!
You will need to integrate it into your d3 environment. The file
is only helpful for you if you (plan to) work with d3 or, for example
if you plan to transcribe the projections to some other software:
d3-geo-projection-code-for-winkeldenner.js.zip
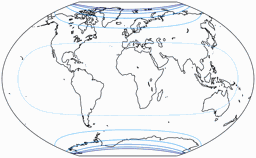
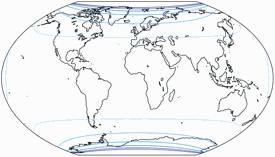
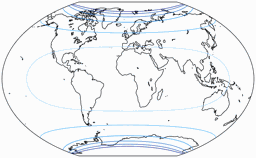
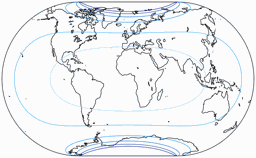
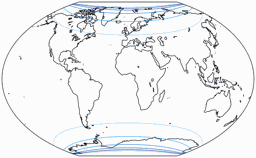
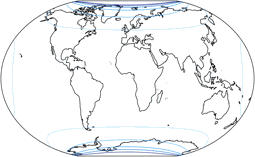
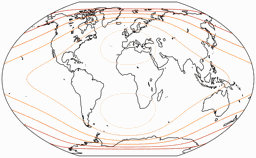
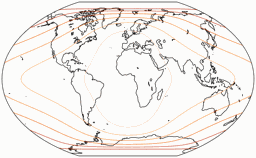
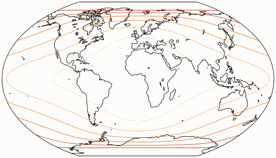
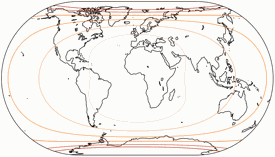
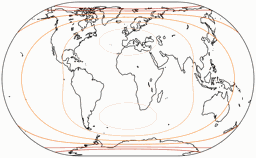
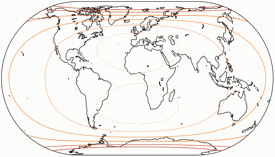
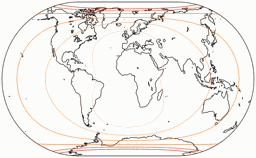
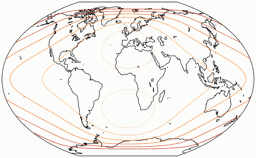
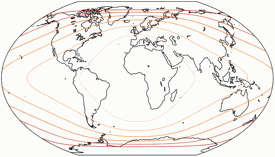
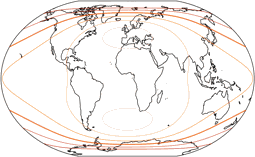
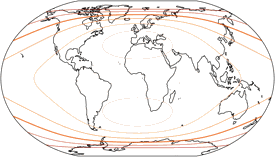
Distortions
Regular visitors to my blog will know: When Peter Denner is involved, distortion plots are not far away! 😉 So here there are – for all seven projections, each one with the standard parallels (of the equirectangular portion) at 50.46° and 40°.
Areal Inflations
The lines are shown at areal inflation values (normalized to the value at the central point of the map) of:
1.2; 1.5; 2.0; 2.5; 3.0; and 3.5.
Angular Deformations
The isolines are given for max. angular deformation of:
10°, 20°, 30°, 40°, 50°, and 60°.
Comparison Matrix
Use the following tables to compare the different variants directly with each other!
Aspect ratio of the original Winkel Tripel
Aspect ratio of the Winkel Tripel Bartholomew
By-products
The source code contains a few by-products: There’s a function for the equirectangular projection that takes a standard parallel (curiously, this function didn’t exist earlier in d3), Peter Denner’s new azimuthal projection – and one that I call Wagner 0[3]: As described above, the Winkelish II was developed using the generalized Wagner VII, but it seemed awkward to use a lenticular projection and then force it into a cylindric projection. So Wagner 0 is a projection that’s cylindrical from the start, but you still can create a continuum of projections with any desired amount of areal inflation between the limiting cases, the cylindric equal area and plate carrée projections. For the Wagner 0 you can apply a reduced variant of the Böhm notation, i.e. Wagner 0 75-180 is having an areal inflation of 1.75 at 60° N/S and an aspect ratio of 1:1.8.[4]
References / Footnotes
- ↑ Aitoff-transformed: Using the transformation that Aitoff used on the azimuthal equal-area projection, i.e. umbeziffert only in the x direction with a limiting meridian of 90°.
- ↑ Actually there is a projection that corresponds to my wishes: The Pavlov cylindric – it even has a very similar amount of areal inflation (1.6 at 60° N/S). But somehow, I kept failing to see it. 😳
-
↑
Wagner 0 = Wagner Zero, not Ooh like Organa.
Wagner I to IX are numbered in the order in which Wagner presented them in his 1949 textbook “Kartographische Netzentwürfe”. But on the pages before that, he used the cylindric equal area projection as an example to demonstrate the process of Umbeziffern incl. “prescribed areal inflation”. Apparently, he didn’t think the result to be a useful map projection, so he only showed the nine well-known projections derived from the sinusoidal, Mollweide and azimuthal projections. This gives me two reasons to call the projection showed here Wagner 0: Its position in the book and the value assigned to it by its author. - ↑ For more information about “Umbeziffern”, Wagner’s transformation method and the Böhm notation, read Das Umbeziffern – The Wagner Transformation Method, or the brief explanation in this blogpost or the notes at the Wagner Variations Generator (WVG-7).
Comments
3 comments
Peter Denner
I'm surprised you say that Winkel-Denner II is a favourite since you normally prefer projections with lower areal distortion.
You do yourself a disservice when you say, "I just said: 'Oh, this does not look very good' and then left it at that." You went on to create the Winkelish II, which is very similar to my Winkel-Denner I. They both improve on the Winkelish I in the same way - by reverting to equally spaced meridians along the equator as in the original Winkel Tripel - and the differences between our two projections are mostly due to the parameter values that you've chosen for the parent cylindrical projection.
Peter Denner
Tobias Jung
I found it very helpful myself. :-)

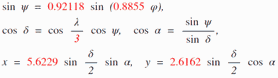
















 Except where otherwise noted, images on this site are licensed under
Except where otherwise noted, images on this site are licensed under
Tobias Jung
> you normally prefer projections with lower areal distortion.
Oh yeah. I meant Winkel-Denner I *blush* and just corrected that mistake. Thank you for 9*********+8 asking! (Additional typing by our cat Sam.)
> You went on to create the Winkelish II
Yes, but in 2018, I left it at that.