Tue Feb 21, 2023 13 Projections for 2023 (Part 2)
A collection of projections for political world maps
(see Intro for further explanations)
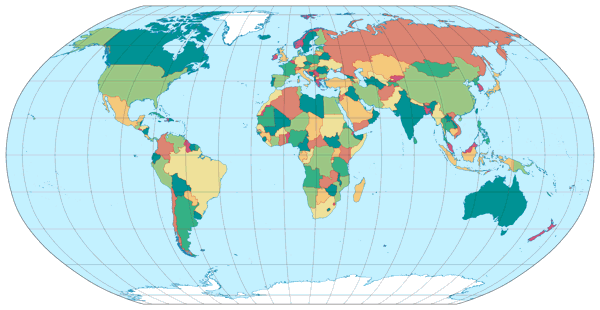
February: Robinson Projection
| Robinson | |
|---|---|
| Creator | Arthur H. Robinson (1963) |
| Group | Pseudocylindric |
| Property | Compromise |
| Other Names | — |
| Remarks | Not based upon mathematical formulas but tabular coordinates providing positions of the meridians and parallels in order to produce a »right-looking« map. |
Sorry for the delay, but various things kept me from writing the February blogpost. In order to get it online before March hits, I’ll make it really short:
As said in the table above, the Mr. Robinson created this projection
in order to produce a “right-looking” map.
And I think he really achieved that goal!
Granted, distortion metrics like the Airy-Kavraiskiy criterion
will usually show that
projections with equally spaced parallels (along the central meridian) – like
Kavraiskiy VII,
Frančula XI,
Györffy B or
Winkel Tripel –
come up with better overall distortion values.
But since (as I’ve said in the January part and probably lots of times before)
I always like a bit less areal inflation near the poles,
the Robinson indeed looks or rather feels “more right” to me.
Moreover, I have seen it used as political map in atlases and on wall maps more than once (for example, in the current edition of Meyers Universalatlas and since years in the CIA World Factbook). When I decided on the leitmotif for the calendar, it was clear to me that the Robinson projection could not be missing.
It also looks very fine in the OGABO version and the plagal aspect:
Remember that I was going to talk about Pacific-centered maps again in the January part of the calendar, but then postponed it to the February part? Well, that will be postponed to the March part…
My 2023 Map Projection Calendar
To read another part of my 2023 map projection calendar series, select the desired month.
Comments
2 comments
Peter Denne
https://www.map-projections.ne…
This raises the question: how closely could a variant of Wagner V approximate the Robinson?
I also think there are plenty of other projections that are more "right-looking". Admittedly, the Robinson does a good job over the populated part of the globe, but high latitudes are severely stretched. Alaska is particularly bad, suffering both from this stretching and from the stubborn refusal of the parallels to bend as they approach the boundary.
Peter Denner
By adjusting the ratio a bit further, you can easily get a lower distortion value for the Robinson than for Kavrayskiy VII, Francula XI or Györffy B, but you have to go really far for the Robinson to have a lower distortion value than the Winkel tripel, which has the benefit of curved parallels.













 Except where otherwise noted, images on this site are licensed under
Except where otherwise noted, images on this site are licensed under
Tobias Jung
Yeah, their similarities are basically the reason that this website even exists, see
https://map-projections.net/wh…
> how closely could a variant of Wagner V approximate the Robinson?
Probably very close, but see for yourself – here’s a quick & dirty implementation of a customizable Wagner V (and others) layered over a Robinson image:
https://map-projections.net/d3…
Select "Mollweide [Var.Id 2]" as Modified Projection.
"right-looking" is of course a very subjective term – that’s why I wrote above that it "feels" more right to me. And I couldn’t even exactly say WHAT it is that makes a projection "look right" to me…
Peter Denner
I settled on 68-60-60-29-197 with a scale of 156. You have to increase the graticule spacing to 15 to get it to line up.
Peter Denner
https://www.giss.nasa.gov/tool…
If you did a Bartholomew on it and reduced the standard parallel of the parent equirectangular projection to 40° or so, or if you took the Bromley instead of the Mollweide, I bet it would look really good - for a pseudocylindrical, that is.
Tobias Jung
Looks like a very good approximation to me (considering that these two projection will always differ to a certain degree)!
> I recently came across the Winkel-Snyder (…) If you did a Bartholomew on it
> and reduced the standard parallel of the parent equirectangular projection to 40°
A while ago, I wrote a Winkel-Snyder implementation for d3.
Here’s the result of your proposed modification:
https://map-projections.net/im…
However, with phi0 = arccos(2/pi) my implementation didn’t match with G.Projector’s image so I’m not certain if it’s a real Winkel-Snyder at all.
I always wanted to explore this further, but … well, I never did.
Peter Denner
If you send me the code for your implementation, I'd be more than happy to check it.