13 Projections for 2022 (Part 5)

Mon May 02, 2022 13 Projections for 2022 (Part 5)

A collection of my own experiments
(see Intro for further explanations)

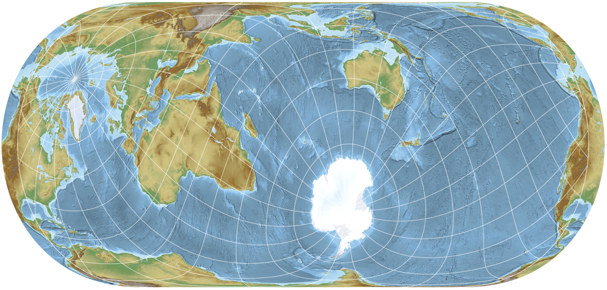
May: Spilhaus-Hufnagel

Spilhaus-Hufnagel
Original Creator	Athelstan F. Spilhaus (1979) / Herbert Hufnagel (1989)
Group	Pseudocylindric
Property	Equal-area
Remarks	The equal-area Hufnagel 10 using the projection center of Spilhaus-Adams.
My variation	Developed in 2021, presented here for the first time

Shortly before I started to work on the 2022 calendar, I stumbled across the Spilhaus-Adams Projection that I presented a few days ago. I instantly liked it, and decided that an equal-area counterpart to Spilhaus’ conformal original will appear in the calendar. After running a series of tests – *hrumph* alright, I think I actually tried three or four projections –, I chose the Hufnagel 10 because of its favorable distribution of distortions. Just line its predecessor, the Spilhaus-Hufnagel can’t show the World Ocean without interruptions, so I used repetitions to extend it on the left and right edges of the map. (In the image above, the graticule and boundary lines tell you where usual bounds of the projection are).

I was quite satisfied with the result and decided to add it to My Projection Collection once I’ve introduced it in the calendar series. But if you now go there to check, you’ll see that the Spilhaus-Hufnagel is not listed.
What happened?

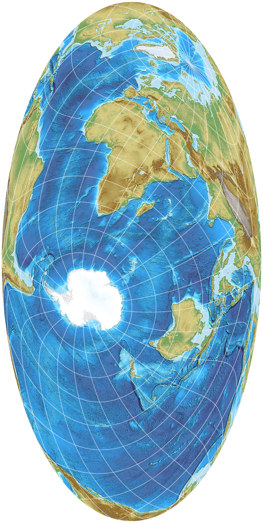
Well, a while later – the calendar had already been printed – I found out that Mr. Spilhaus already had presented an equivalent projection using that specific map center^[1]^[2] – namely an oblique aspect of the Spilhaus-Hammer Projection that I also presented the other day. Having realized that, it felt unnecessary to add my own variation of the theme. Instead, I renamed the Spilhaus-Hammer to Spilhaus-Hammer I, and added Spilhaus’ oblique version, calling it Spilhaus-Hammer II.

As always, the projection is shown in landscape orientation in my Projection Collection, but here it is in portrait orientation, which is the way Mr. Spilhaus presented it:

And by the way: I screwed up when I tried to show the World Ocean without any interruptions in the Spilhaus-Hufnagel. As you can see in the enlarged details below, I managed to cut off a few pixels of the Bohai Bay in the Yellow Sea. 😳
Oh well – at least, this way I learned that there is a bay called Bohai which, as I hate to admit, has so far escaped my attention.

Next month, you will have read the entire blogpost before you can say blueberry pie.

References / Footnotes

↑ Spilhaus, A. (1983): “World ocean maps: The proper places to interrupt.” Proceedings of the American Philosophical Society, 127 (1), p. 50–60
jstor.org/stable/210385 (free access after registration)
↑ Spilhaus, A. (1991). “Atlas of the World with Geophysical Boundaries: Showing Oceans, Continents and Tectonic Plates in Their Entirety”. Independence Square, Philadelphia: The American Philosophical Society.
Accessible at Google Books