13 Projections for 2022 (Part 10)

Sun Oct 02, 2022 13 Projections for 2022 (Part 10)

A collection of my own experiments
(see Intro for further explanations)

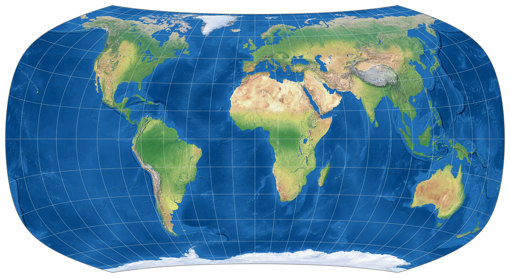
October: Canters W30/UA (non-optimized)

Canters W30/UA (non-optimized)
Original Creator	Frank Canters (2002)
Group	Lenticular
Property	Compromise
Remarks	An umbezifferte (renumbered), aphylactic (= compromise) variant of Canters W30. Not optimized for low distortion values.
My variation	Developed in 2021, presented here for the first time.

I’ve listed some of Frank Canters’ projections ever since my website was launched in 2015. Successively, I added more of them in the following years. In 2021, I completed the full set of all world map projections presented by Canters in his 2002 textbook^[1] and reviewed them in a two-part article.^[2]

Among them, there was the projection Canters W30^[3] (an equal-area transformation of Wagner VII), which has comparatively good distortion values (according to Canters’ own metric):

Canters W30

I like this projection, but it surely looks quite unusual. Maybe a bit of Umbeziffern^[4] would help to relax the odd shape? Worth a shot! I didn’t change the length of the pole line but set the bounding meridian to 150°E/W. The result was an equal-area map that looked promising (I will come back to this in a moment). Then, I added some areal inflation (1.35 at 60°N/S) and horizontal compression (by setting the ratio of the main axes to 1:1.8 instead of 1:2) – voilà, that’s the configuration you see at the top of this blogpost!

If I had the means to measure the overall distortion values or at least to create the isolines of angular distortions and areal inflations I would have experimented further. But I haven’t, therefore I left it at that. In my opinion, this variant was good enough to be put to the calendar – and to my Projection Collection as well, so I added it today, along with the intermediate equal-area variant I mentioned above. In terms of the overall distortions, my guess is that both of them are nothing special, but not too bad either.

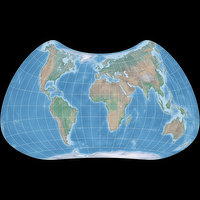
The equivalent variant:
Canters W30/UE (non-optimized)

As for naming the two projections: In the printed version of the calendar, I called the projection Canters W30/UA (U for umbeziffert, A for aphylactic). Consequently, the equal-area variant would be Canters W30/UE…
But then I had some doubts. Frank Canters did most of the work, so it’s appropriate to name the projection after him. On the other hand, all of Canters’ projections are mathematically optimized for low distortion values. Using his name may cause the misconception that my variants were optimized in the same way, which is definitely not the case. How could I resolve this contradiction? After thinking about this for a while, I realized that it’s impossible to use Canters’ name and not use it at the same time 😉 so I followed Peter Denner’s suggestion to add the suffix “(non-optimized)”.

The remaining two projections of this year’s calendar are not new, I already presented them to you.
And by the way, currently I’m not sure if there will be a 2023 calendar. Mostly because I’ve no idea for a leitmotif. In case you’ve got an idea, please post it in the comments below.

References / Footnotes

↑ Frank Canters:
Small-scale Map Projection Design.
London & New York 2002.
↑ See The Canters Projections, Part 1 and Part 2.
↑ Canters himself called this projection Low-error equal-area transformation of Hammer-Wagner with twofold symmetry and correct ratio of the axes, but I adopted the naming scheme presented by Dr. Rolf Böhm. For more information on that matter, see Naming Canters’ Projections.
↑ For more information about “Umbeziffern”, Wagner’s transformation method, read Das Umbeziffern – The Wagner Transformation Method, or the brief explanation in this blogpost or the notes at the Wagner Variations Generator (WVG-7).