13 Projections for 2023 (Part 8)

Wed Aug 02, 2023 13 Projections for 2023 (Part 8)

A collection of projections for political world maps
(see Intro for further explanations)

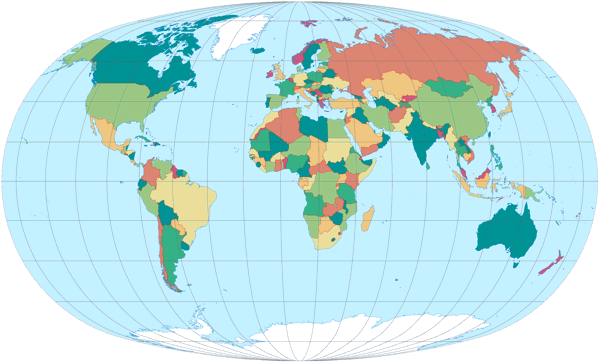
August: Baranyi IV

Baranyi IV
Creator	János Baranyi (1968)
Group	Miscellaneous
Property	Compromise
Other Names	—
Remarks	Constructed with tabular coordinates rather than mathematical formulas. Meridians are not equally spaced along a given parallel, therefore it doesn’t fall in to the pseudocylindric group of projections. See my blogpost Two Ginzburg and four Baranyi Projections.

I’ve introduced this projection in the blogpost I’ve linked to above.
I’ve shown contour plots of distortions in the Adams, Baranyi, Winkel-Snyder blogpost.
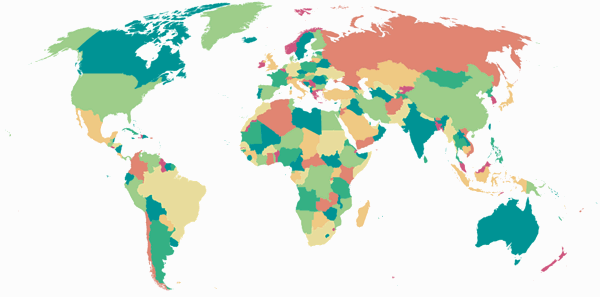
Is there anything else I can say? Yes – strangely enough, while I like Baranyi IV as portrayed in the calendar, I like it less in the OGABO version. I can’t even tell why, I just feel … uncomfortable about it:

I mean – of course I know that the areal and angular distortions of the Arctic regions bother me. I just don’t know why they bother me more in the OGABO version than in the other.

That was the last projection of the year that I actually saw in use as a political map. The remaining four, however, would qualify for that in my eyes. Two of them follow a more traditional approach and the other two … do not.
Bis die Tage!