Tue Dec 05, 2023 13 Projections for 2023 (Part 12)
A collection of projections for political world maps
(see Intro for further explanations)
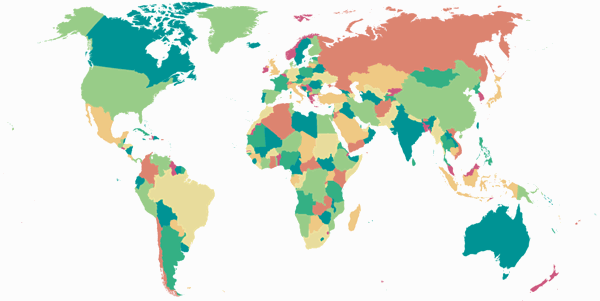
December: Frančula XIII
| Frančula XIII | |
|---|---|
| Creator | Nedjeljko Frančula (1971) |
| Group | Lenticular |
| Property | Compromise |
| Other Names | — |
| Remarks | A Wanger IX variant, derived by Umbeziffern from the equatorial azimuthal equidistant projection, minimized distortion by application of the Airy-Kavrayskiy criterion. For more information, refer to my blogpost The Frančula Projections or Frančula’s original paper Die vorteilhaftesten Abbildungen in der Atlaskartographie (German). |
If I had known a year ago that this would be the last projection calendar, I would have chosen one of my own experiments for December, but I hadn’t made the decision at that point. However, having a Frančula projection here is the second best idea. At the risk of sounding boastful, I was the one who dug up the projections by Nedjeljko Frančula and presented them to the public. Of course I wouldn’t have known about them if they wouldn’t have been briefly mentioned by Györffy[1], and I wouldn’t have been able to show them to you with the help of Peter Denner, but well, the fact remains that the 14 projections (as far as I know) have never been shown before, save for Frančula’s own paper. So I have a personal attachment to the last projection in the series, even if I didn’t create it myself. 🙂
Frančula XIII is an aphylactic lenticular projection with a pole line and equally spaced parallels along the central meridian, just like the Winkel Tripel Bartholomew (July) and Canters W09 (September). So I may have gone a little overboard with this category in the calendar, but I do think that it works well with political maps.
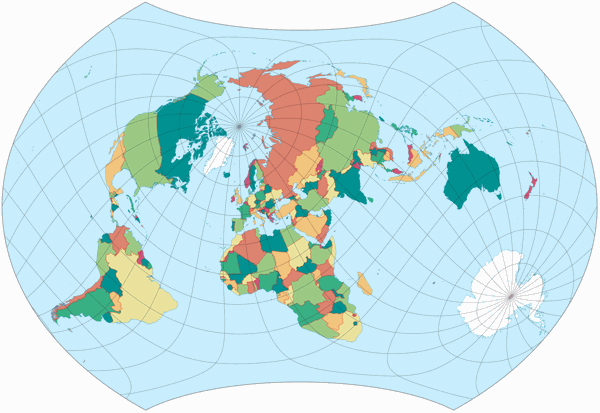
Hence it’s not surprising that, as with Winkel and Canters, I find Frančula XIII also very usable in the OGABO version and the plagal aspect:
Th-th-that’s all, folks!
But only for my projection calendars, so – see you soon!
References / Footnotes
-
↑
János Györffy: Minimum distortion pointed-polar projections for world maps by applying graticule transformation
doi.org/10.1080/23729333.2018.1455263
My 2023 Map Projection Calendar
To read another part of my 2023 map projection calendar series, select the desired month.
Except where otherwise noted, images on this site are licensed under
Comments
Be the first one to write a comment!