13 Projections for 2023 (Part 6)

Tue June 06, 2023 13 Projections for 2023 (Part 6)

A collection of projections for political world maps
(see Intro for further explanations)

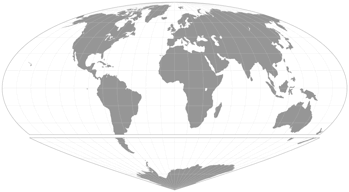
June: Philbrick Sinu-Mollweide

Philbrick Sinu-Mollweide Uninterrupted
Creator	Allen K. Philbrick (1953)
Group	Pseudocylindric
Property	Equal-area
Other Names	—
Remarks	Often shown interrupted.

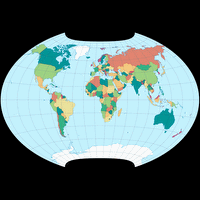
Philbrick’s projection is a fusion of the sinusoidal projection with the Mollweide at the 40°44′S. The result is rotated to be centered at at 55°N 20°E. It is usually shown with interruptions.

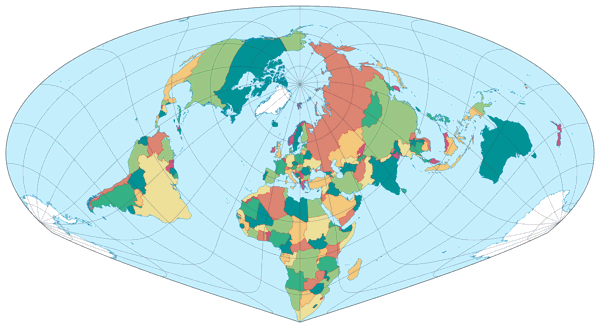
And there it is, the first unusual projection of the year – except that it probably doesn’t seem so unusual now, because I’ve shown all the previous projections in the plagal aspect, centred on 36°N/45°E/37°. But I didn’t know that I was going to do that when I built the calendar.

Is it advisable to use such an unusual projection for a political map? Probably not in an atlas. It would be more appropriate to use it as a wall map: Even if you want to use it mainly as a source of information, it can’t hurt if it also looks appealing, can it? The position of the countries in the northern hemisphere (or perhaps rather in the northern half of the northern hemisphere) relative to each other is shown better than on the usual maps in equatorial aspect – that may be helpful for various articles and reports.

However, the Sinu-Mollweide projection has further benefits: It shows all continents except Antarctica without interruptions and has a very advantageous distribution of angular distortions for an equal-area projection; almost all land areas (apart from Antarctica again) remain below 40°. I only find the pointed South Africa rather disturbing.

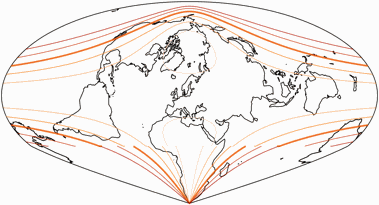
The isolines are given for max. angular deformation of:
10°, 20°, 30°, 40°, 50°, and 60°.
Discontinuities in the lines are a consequence of the fusion.

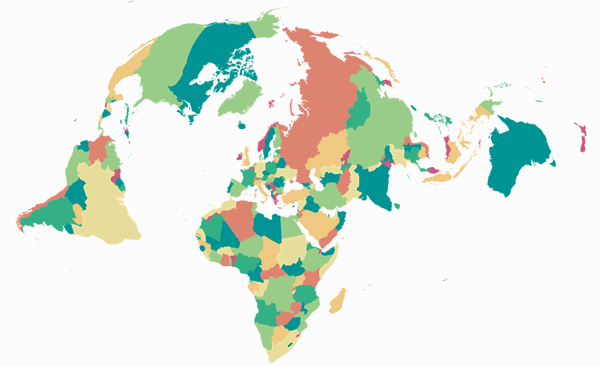
Perhaps it is these low angular distortions that make me feel that even the OGABO version works well. Or maybe it’s just the fact that Africa and Europe remain centred and keep the shape that I’m used to. I don’t know. But I had expected that this type of representation would not fit the Sinu-Mollweide projection at all – but I think it does: