13 Projections for 2023 (Part 4)

Tue Apr 18, 2023 13 Projections for 2023 (Part 4)

A collection of projections for political world maps
(see Intro for further explanations)

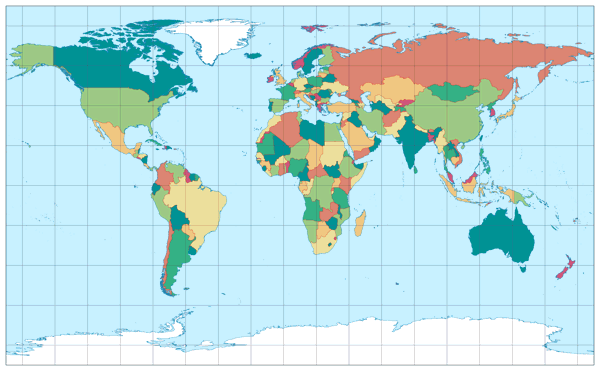
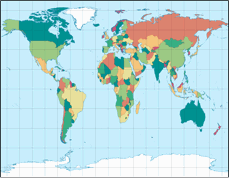
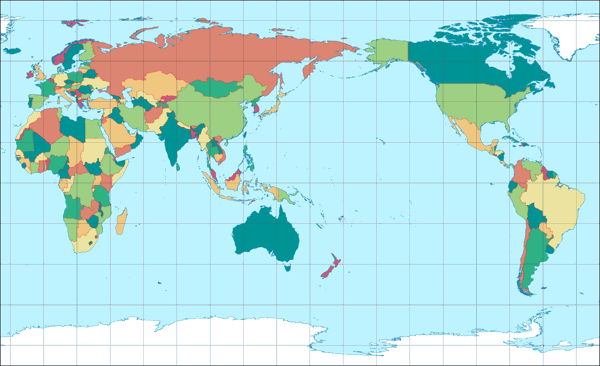
April: Equirectangular Projection

Equirectangular Projection
Creator	Marinus of Tyre (about AD 100)
Group	Cylindric
Property	Equidistant
Other Names	—
Remarks	Here: Standard parallels at 35° North/South.

Usually I am not very enthusiastic about cylindrical projections. But given the fact that I built a labelled political world map myself a few years ago, and decided on a cylindrical projection for good reasons – and it’s a map that I use regularly for reference –, I can hardly discourage the use of this group of projections, huh?

Moreover, as I’ve said time and again, people seem to love rectangular world maps in general and in particular those having straight meridians and parallels (i.e. the cylindrical projections). The mathematically simplest (and even simplest possible) projection of this kind is the equirectangular projection, and in my opinion it is nonetheless more suitable for many purposes than other cylindrical projections. If you look at other (non-equivalent) cylindrical projections, you’ll see that most of them^[1] have a significant higher amount of areal inflation towards the poles – too much for most uses if you ask me.

By using standard parallels^[2] the equirectangular projection can be compressed horizontally. In the image shown above I decided on 35° N/S, because this way, the map fitted perfectly into the available space of the calendar sheet. Ans I was quite happy about that because in my opinion, you get the best results with the standard parallels between 30° and 40°.

Just for the fun of it, we’ll look at this little sequence, showing the equirectangular projection with standard parallels at 0, 10, 20, 30, 35, 40, 45, 50 and 60 degree:

The first variant, using the equator as standard parallels (this case is also called plate carrée projection), is in my opinion … well, quite okay, although the east-west stretching of the polar areas is almost painful. At least it has the correct ratio of the main axes – which disappears on the variants with 10° and 20°, but without a noticeable improvement regarding the distribution of distortions.

Standard parallels at 30, 35, 40 degree: These are configurations that I would recommend to be used for a political map. 45° (this variant is also known as Gall Isographic) already lead to an awkward North-South stretching in my eyes; although I’m aware according to that certain distortion metrics, standard parallels in that area are optimal.^[3]

Using 50° N/S as standard parallels results in a map that’s quite ugly. It’s only included in this sequence so I can still get to the 60° variant, which produces an exactly square map. Admittedly, I don’t know why anyone should want something like this, but I’m sure it happens, so – here is a square map.

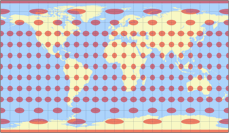
Since I mentioned the distribution of distortions, I’ll show the same variants as above again, but this time presenting the Tissot indicatrix:

And since this blogpost still doesn’t have enough colourful pictures, here’s the OGABO version, and maps with the two projections centers mentioned in Minimizing the Severing of Land, namely the plagal aspect and centered to 154° East:

The OGABO version of course always works well on cylindric projections. The plagal aspect is quite favourable to most parts of the land. And the 154°E version – well, in the “Minimizing” blogpost mentioned above, I said that there is “a catch with the pacific-centered maps”. The catch is that this center works well only with cylindric projections. Other types of projections push the distortions to the edges of the map, i.e. into the Pacific Ocean when centered at or close to the Greenwich meridian. Unfortunately, there are continents at the edge of the map when it is centered to the Pacific.

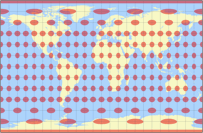
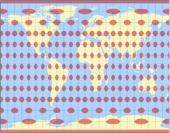
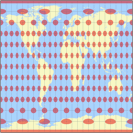
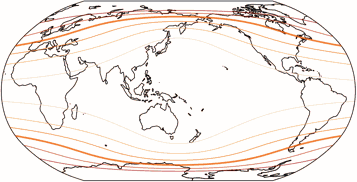
Compare the distribution of angular deformations in Robinson (our February projection), Wagner VII (March) and the equirectangular projection – and you’ll see why it’s highly advisable to chose a cylindric projection for pacific-centered maps:

The isolines are given for max. angular deformation of:
10°, 20°, 30°, 40°, 50°, and 60°.

In May we’ll have a projection, that has never been used anywhere (to my knowledge) although it’s absolutely not an “unusal” one.

References / Footnotes

↑ “Most of them”? Nope, all of them except the Patterson projection.
↑ The standard parallel is the parallel that is at the correct scale, or – in this case – is shown in the correct aspect ratio compared to the meridians.
↑ See Peter Denner’s posting in the Mapthematics forum, and “Atarimaster’s” (that’s me) reply.