Fri Apr 03, 2020 12 Projections for 2020 (Part 4)
To understand what this is about, you should read the intro.
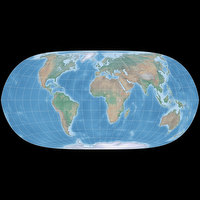
April: Strebe-Mollweide
| Strebe-Mollweide | |
|---|---|
| Creator | Daniel »daan« Strebe (1992) |
| Group | Lenticular |
| Property | Equal-area |
| Other Names | — |
| Remarks | Transformation of the Mollweide projection, using Bonne φ1 = 16°N. Read my blogpost for more information. |
I’ve handled Strebe’s 1992 series of equal-area projections in detail in the blogpost linked to in the table above. So for now, I think it’s sufficient to summarize:
The Strebe-Mollweide is a pointed-pole projection which at first glance looks like a projection having a pole line. That’s interesting because I think that to a lot of people (including myself) a pole line looks & feels more »natural« (although it actually isn’t), however an equal-area pointed pole projection usually is better at showing both Africa and Greenland with tolerable distortion of shapes – which of course is nothing more than a personal preference. I simply like it when this is achieved but it is in no way an »objective« basis of assessment.
The projection has its drawbacks: Alaska looks quite squished, and the meridians’ kinks at the equator were described as »undesirable« by the author himself. Nonetheless I think that it’s an usable equal-area projection that deserves some more attention.
Next month, we’ll have another equal-area projection, but it’s going to be quite different.
I wish you all the best in these testing times!
For the Strebe-Mollweide image in the calendar, I used a slightly modified version of the Natural Earth Cross-blended Hypsometric Tints. Projected with Geocart.
Except where otherwise noted, images on this site are licensed under
Comments
Be the first one to write a comment!