12 Projections for 2020 (Part 7)

Wed July 01, 2020 12 Projections for 2020 (Part 7)

To understand what this is about, you should read the intro.

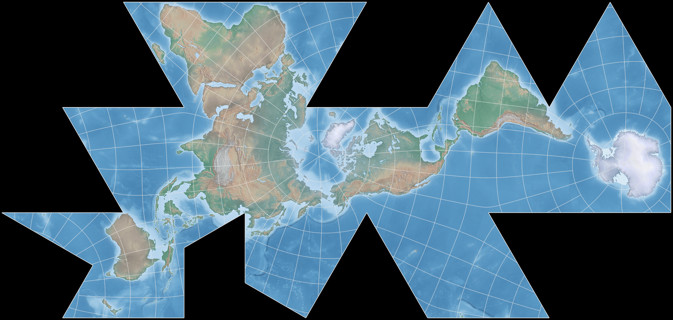
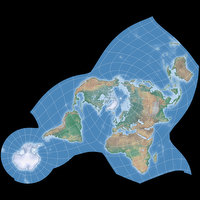
July: Dymaxion-like Conformal Projection

Dymaxion-like conformal projection
Creator	Daniel »daan« Strebe, Buckminster Fuller, Oscar S. Adams, L.P. Lee (1943 / 2019)
Group	Polyhedral
Property	Conformal
Other Names	—
Remarks	Arrangement by Buckminster Fuller in 1943. Fuller’s projection was not conformal. Mathematical work on conformal projections for regular polyhedra largely originated with Oscar S. Adams from 1925 and onward. L.P. Lee greatly expanded upon and regularized the mathematics in 1976. This application of conformal developments to Fuller’s arrangement is by Daniel “daan” Strebe in 2019.

This time, I can make it really short and sweet, because I already talked about this projection a year ago.
And the only thing I might add is that I still think that the dymaxion-like conformal is better than the original projection.

So, this was the last conformal projection for this year. Next month, I’m going to show you an aphylactic (compromise) projection – one that looks much more commonplace, although to my knowledge it is rarely used (with one exception).

For the image in the calendar, I used a slightly modified version of the Natural Earth Cross-blended Hypsometric Tints. Projected with Geocart.