14 Projections for 2021 (Part 12)

Sat Dec 11, 2021 14 Projections for 2021 (Part 12)

If you wonder what this is about at all, you probably didn’t read the intro.

December: F13 Copycat

F13 Copycat
Creator	Karlheinz Wagner, Tobias Jung (1941 / 2020)
Group	Lenticular
Property	Compromise
Other Names	Wagner vii@60-77-60-45-170
Remarks	Wagner VII variant, configuration 60-77-60-45-170 (using the Böhm notation, see Umbeziffern – The Wagner Transformation Method. Experimental, a Frančula XIII copycat, with bit less areal inflation. Briefly introduced in my blog.

This month, the selected projection is the F13 Copycat, one of my own experiments. I introduced it a year ago in the blogpost about the Frančula projections (see link above) – and that’s how it got its name, because it’s a copycat of the Frančula XIII.

Everything else is basically mentioned in the blogpost, so there’s no need that I get chatty here … no, wait, there is a thing: I mentioned that the F13 Copycat has good distortion values according to Capek’s Q^[1] but meanwhile, thanks to Peter Denner, I know that is also is quite decent according to the metric of Goldberg & Gott^[2] and the Airy-Kavrayskiy criterion.

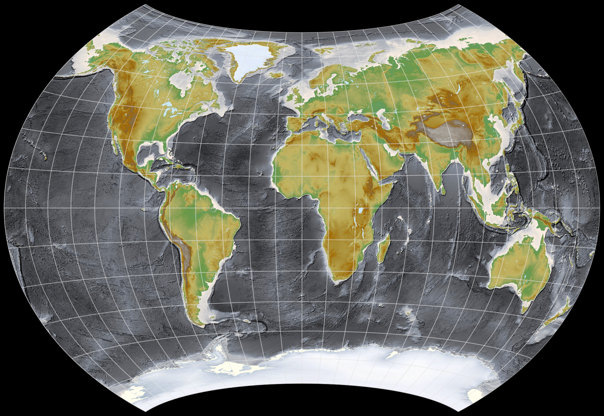
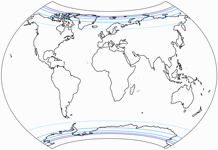
Here are images showing isolines of angular deformations and areal distortions, once again provided by Peter Denner. 🙏
The isolines are given for max. angular deformation of:
10°, 20°, 30°, 40°, 50°, and 60°.
For the areal inflation, shown normalized to the value at the central point of the map, the lines represent values of:
1.5; 2.0; 2.5; 3.0; and 3.5.

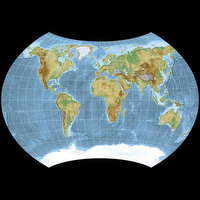
But – this isn’t the projection I actually showed on the December sheet of the calendar! There, I used another one of my own experiments, namely Wagner BCW-A I:

Last I year, I chose this projection because – well, firstly because I always like to smuggle in one or two of my own projections. 😉 Secondly, because the BCW-A I has a very decent Q value: 82.4, which would be rank #5 in Capek’s list of 100 projections. But it turned out that the distortion values according to Goldberg & Gott and the Airy-Kavrayskiy criterion aren’t that great. And so, I chose to cheat a bit and pretend I presented a better one …

So. We are through with that.
We have ploughed through the entire 2021 calendar. I hope you had a bit of fun. If so, you will be might to learn that there will be a 2022 calendar! Once again I decided to use a leitmotif for the calendar. I will reveal what it is in January.

See you!