14 Projections for 2021 (Part 3)

Mon Mar 01, 2021 14 Projections for 2021 (Part 3)

If you wonder what this is about at all, you probably didn’t read the intro.

March: Winkel Tripel Bartholomew

Winkel Tripel Bartholomew
Creator	Oswald Winkel (1921)
Group	Lenticular
Property	Compromise
Other Names	Winkel Tripel Times Atlas Winkel Tripel φ₀ = 40°
Remarks	This version was designed by John Bartholomew (about 1955), it uses 40° North and South as standard parallels instead of 50°28´ in Winkel’s original design.

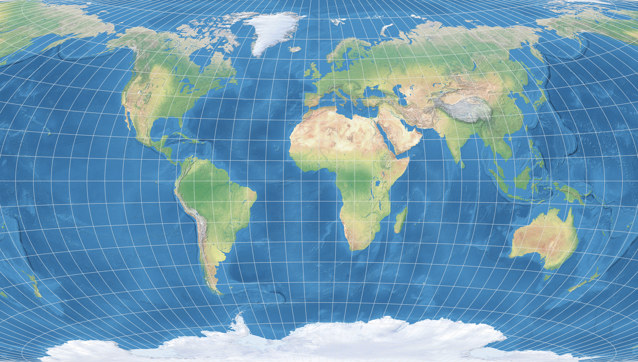
This month, we’ve got a real classic: The Winkel Tripel (Bartholomew variant), which is frequently used in atlases, for wall maps or thematic maps in newspaper magazines etc.
Moreover – and more importantly in terms of this calendar – it’s always among the best projections by various of the comparison schemes that I mentioned in the intro. And more often than not, it’s even the best projection of the “well-known” ones (which usually refers to projections that were developed before the age of low-error projections that were obtained with the help of computers). This holds true both the original Winkel Tripel and the Bartholomew variant.
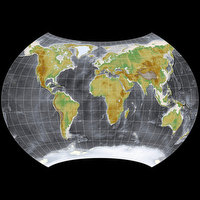
Compare Winkel Tripel Original and Winkel Tripel Bartholomew

Usually both variants are shown having a “bowl-shaped” form, but above you can see a rectangular shape: I chose to use a representation that, as I mentioned in February 2020, often is used for the van der Grinten I: The projection is extended beyond its usual boundaries, repeating certain parts in the east and west until they fill up a rectangular space.

I have to say that I’m not too fond of this technique – but I already had both Winkel Tripel variants in previous calendars, so I at least wanted to show a different representation this time.
I guess I do not even have to mention that the advantageous distortion characteristics only occur within the usual bowl-shaped boundaries while the distortions in the repeated parts are severe.

So that’s it for this month… Wait, didn’t I promise a substantially longer blogpost last month?
I did. But I changed my mind and decided that it’s better if the other things I want to say about the Winkel Tripel will be presented in a separate blogpost. I’ve already started to write it so hopefully, it’ll be available before too long.

Next month, we’ll see one of the aforementioned low-error projections that were obtained with the help of computers.

References

↑ János Györffy, 2018: Minimum distortion pointed-polar projections for world maps by applying graticule transformation
doi.org/10.1080/23729333.2018.1455263